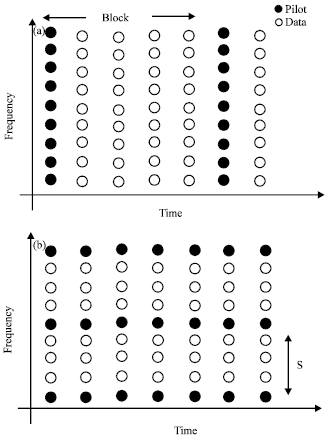
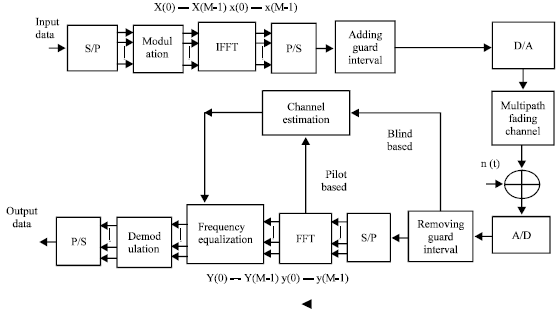
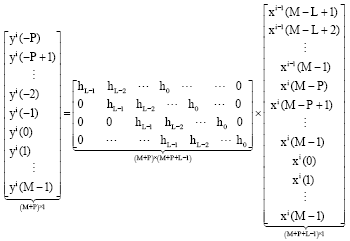
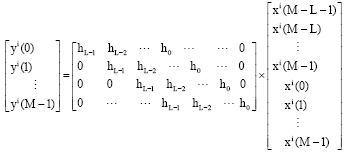
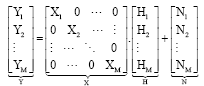
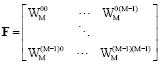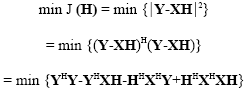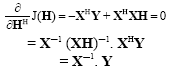Review Article
Review on Selected Channel Estimation Algorithms for Orthogonal Frequency Division Multiplexing System
College of Information and Communication Engineering, Harbin Engineering University, No.145, Nantong Str. Nan gang Dist, Harbin, 150001, 21-A Building, Communication and Circuit Lab, R553, Peoples Republic of China
Jiang Tao
College of Information and Communication Engineering, Harbin Engineering University, No.145, Nantong Str. Nan gang Dist, Harbin, 150001, 21-A Building, Communication and Circuit Lab, R553, Peoples Republic of China
Wei Zhang
College of Information and Communication Engineering, Harbin Engineering University, No.145, Nantong Str. Nan gang Dist, Harbin, 150001, 21-A Building, Communication and Circuit Lab, R553, Peoples Republic of China