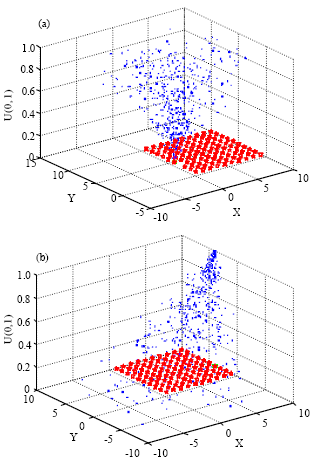
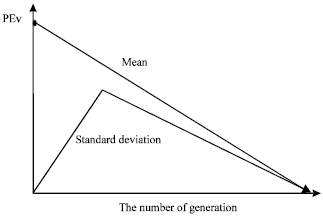
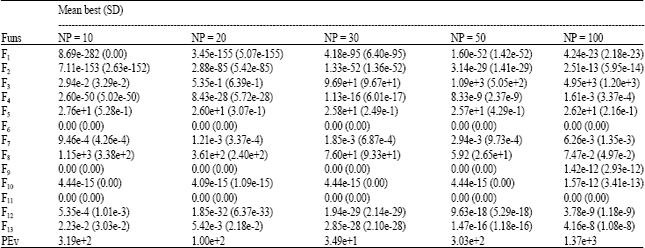
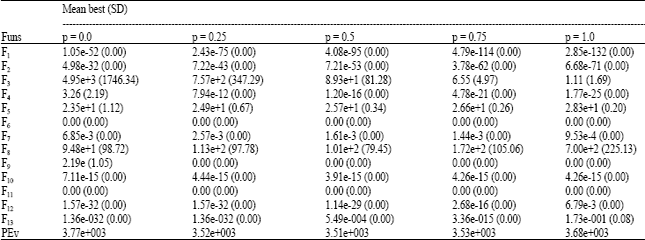
Research Article
A New Differential Evolutionary Algorithm with Neighborhood Search
School of Mathematics and Computational Science, Xiangtan University, Xiangtan, People�s Republic of China
Shoufu Li
School of Mathematics and Computational Science, Xiangtan University, Xiangtan, People�s Republic of China