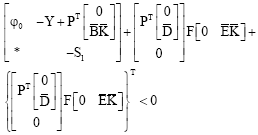
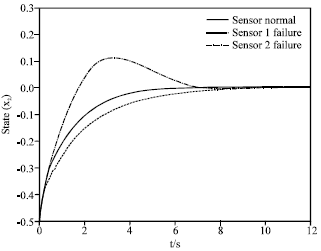
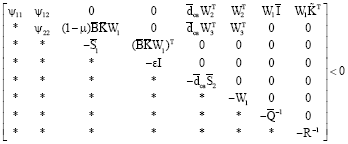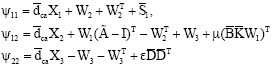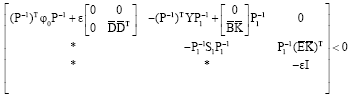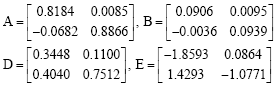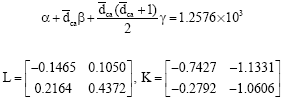Research Article
Observer-based Guaranteed Cost Fault-tolerant Controller Design for Networked Control Systems
College of Engineering, Huazhong Agricultural University, Wuhan, China
Xiao-Bei WU
Institute of Automation, Nanjing University of Science and Technology, Nanjing, China
Jian Gao
Wuhan Second Ship Design and Research Institute, Wuhan, China