ABSTRACT
These recent years, Low Earth Orbit (LEO) satellite networks, which have global coverage and short round-trip delays, have been playing an increasingly important role. As fast speed, frequent handover and time-varying topology, to develop specialized and efficient routing algorithm is a huge challenge in LEO satellite networks. A Distributed Routing Algorithm with Traffic Prediction (TPDRA) is proposed in this study. TPDRA solves the linearly inseparable problem of satellite traffic prediction in higher dimensionality space and finds the optimal path for data packets through mobile agents. TPDRA consists of two parts, traffic prediction and routing decision. In traffic prediction module, the upcoming traffic from terrestrial is forecasted using Radial Basis Function neural network. In routing decision module, mobile agents traverse the whole satellite networks and collect the routing information. The final routing decision factor is not only depending on the current state of satellite networks, but also related to the future state of satellite nodes. Simulation shows that, compared with ACO, TPDRA has better transmission delay as well as intensive performance for congestion.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/itj.2011.285.292
URL: https://scialert.net/abstract/?doi=itj.2011.285.292
INTRODUCTION
Satellite systems which provide seamless coverage have become an important component of the next generation global personal communication system (Darnopykh, 2010). Compared with the geostationary orbit (GEO) and the Medium Earth Orbit (MEO) satellites, the propagation delay of LEO satellites is shorter and a few tens of satellites on several orbits are able to provide global coverage. In a LEO satellite system, satellites can directly communicate with each other by using Inter-Satellite Links (ISLs) which can be utilized to transmit network management signal as well as data packets. Due to the time-varying and dynamic topology of satellite networks, to design and realize dynamic adaptive routing has been a challenging issue (Jinglin et al., 2009).
In recent years, some routing algorithms for LEO satellite networks have been developed assuming a connection-oriented network structure (Uzunalioglu et al., 2000). These algorithms use offline computations and satellites actually serve as a transponder, while the optimal paths from a source node to a destination node are only computed on the ground station. Satellites only forward the packets according to the routing tables. In other words, these routing algorithms are static and centralized processing. As a result, their robustness is weak due to the frequent handover in LEO satellite networks. In addition, centralized-processing of the ground station for routing cannot adapt to the overwhelming development of multimedia services. Therefore, dynamic, distributed and adaptive routing is another feasible method for LEO satellite networks. As an inevitable trend, multimedia services are often carried over IP because it has the advantages of favorable expansibility and compatibility. A lot of work is focused on Internet-based application (Wood et al., 2001) and many routing methods considering satellite IP services are presented. Ekici et al. (2001) proposed a distributed routing algorithm (DDR: Distributed Datagram Routing) dealing with the combination problem of IP with LEO satellite networks. To minimize the packet delay, in this algorithm, each satellite is represented by a discrete geographical coordinate and executes routing strategy respectively. But in case of satellite or ISLs broken down, the performance of DDR will drastically deteriorate.
A novel distributed routing algorithm with traffic prediction (TPDRA) is proposed in this paper. In TPDRA, Neural Network (NN) is used to forecast the traffic of satellite nodes, while mobile agents take charge of collecting network information which is used to guide transmission of data packets. Routing decision is not only related to the current state but also the future state of the network. When the bursty traffic is coming, the sudden change can be predicted by TPDRA and advance notice will be received by satellites node. Routing decision strategy increases or decreases the traffic from adjacent satellite nodes to avoid disaster and the congestion probability of satellites is reduced.
ROUTING PROBLEM IN SATELLITE NETWORKS
Routing in satellite networks is essentially an optimization problem which can be divided into two associated parts: path exploring and path maintaining. Any routing algorithms need to collect network information for routing decision. But information collecting always lags behind the change of network. As a result, routing decision strategy has to use the hysteretic information. As a heuristic inspiration, if routing information can be forecasted, the performances of a routing algorithm will be highly improved.
According to historical data and the related information, prediction is a process using proper methods and techniques for the scientific analysis, computation and inference for future situation. At present, statistical regression analysis, time series forecasting and wavelet prediction are commonly-used prediction algorithms. As satellite networks cover the entire surface of the earth, the local time of subsatellite point, population distribution and development of economy are quite different more often than not. Besides, the non-uniform geographical distribution also influences traffic characteristics in satellite networks. These factors and the nonlinear combination of these factors make traffic prediction so complicated that these prediction algorithms are hardly appropriate for traffic prediction in satellite networks. As a hotspot of intellective control method, artificial Neural Network is extensively applied in many frontiers because it has the advantages of self-study, self-adapting and parallel processing. According to combination and simulation of the hidden layer calculation unit in neurons, NN can effectively organize the relationships between independent and dependent variables. In particular, NN is highly effective and suitable for non-linear situations. Therefore, NN is adopted by this paper for the traffic prediction in satellite networks.
In some routing algorithms, once parameters of satellite constellation are set, the topology of satellite networks can be calculated. In fact, the parameters of satellite constellation are fixed, i.e., these settings are static. However, not only the dynamic characteristics of satellite networks can not be reflected such as time-varying network topology, but the change of traffic can not be depicted. A undoubted fact is that traffic of different zones is often quite distinct. When satellites continuously fly over continents and oceans, changes of traffic should be considered into routing algorithms of satellite networks. By means of NN, if traffic of satellite networks is predicted, network resource utilization can be improved. In addition, routing algorithms with traffic prediction proactively deal with changes of network avoiding passively responding to external changes so that the reliability and robustness of the whole network are strengthened.
DISTRIBUTED ROUTING ALGORITHM WITH TRAFFIC PREDICTION (TPDRA)
The proposed routing algorithm with traffic prediction can be divided into two stages, traffic prediction and routing decision.
Traffic prediction: When a satellite moves at high speed on its orbit, the track of subsatellite point will shift due to the earth rotation. Furthermore, the earth surface condition is complex more often than not. These factors complicate the traffic prediction in satellite networks, especially for LEO satellite networks. In this paper, two assumptions are introduced. One is that the state of satellite node is related to its traffic load. In other words, the traffic density of satellite node depends on the queue length of link at satellite node and the ISL capacity. The closer the queue length to ISL capacity is, the busier satellite node is. Another is that the traffic load of satellite node can be divided into two parts: the traffic from the ground and the traffic from adjacent satellite nodes. The former is determined by the objective factors including land and ocean, population, economy development. For the latter, the traffic from adjacent satellite nodes is dependent on routing algorithm, because a well-designed routing algorithm can regulate traffic. Specifically, if the traffic in an area under subsatellite point is high, nodes around the satellite avoid forwarding data by the satellite. If the traffic in an area under subsatellite point is low, for instance over the Pacific Ocean, nodes around the satellite should fully forward data through the satellite. TPDRA is responsible for control and regulation of traffic. The essence of TPDRA is to revise the traffic from adjacent satellite nodes by predicting the traffic from the ground using NN and finally maximize the utilization of satellite network resources.
The potential traffic density from the ground is related to ground conditions. Here it is calculated as follows: the earth surface is divided into a regular grid of cells along with latitude and longitude. The potential traffic density of every square region is determined by the local population and GNP (Kim et al., 2001). In this study, a feasible and convenient idea is introduced that the potential traffic of square region ranges from 1 to 10 in Fig. 1. (Of course, other ranges are accessible with the same idea). The actual traffic from terrestrial received by each satellite is calculated through summing up the densities of the square regions covered by the satellite. In each square region, Radial Basis Function Neural Network (RBFNN) is proposed for traffic prediction (Lee and Shih, 2007).
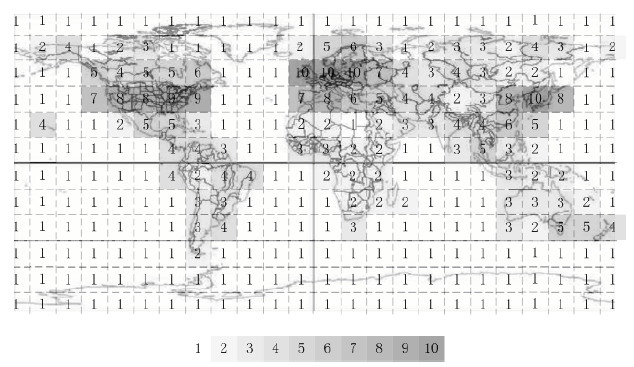 | |
| Fig. 1: | Potential traffic density of earth surface |
| • | The network structure of RBFNN |
RBFNN belongs to multilayer forward neural network in structure and it has three layers. The first layer is the input layer which is composed by the signal source nodes. The middle layer is the hidden layer. The last layer is the output layer which responds to the input mode.
According to Fig. 2, the number of training sample is N. There are M neurons in the input layer and any neuron is denoted by m. The hidden layer has N neurons and any neuron is denoted by i. φ(X,Xi) is the output drive of hidden unit i and represents the basis function. ti = [ti1, ti1,…,tim,…,tiM,](i = 1,2,…,I) is the centre of the basis function. There are J neurons in the output layer and any neuron is denoted by j. The synaptic weights connected hidden layer and output layer is denoted by wij (i = 1,2,…,N, j = 1,2,…,J).
X = [X1, X2,…,Xk,…,XN]T represents the training sample set and any training sample is denoted by Xk = [xk1, xk2,…,xkm,…,xkM], (k = 1,2,…,N). The corresponding actual output is denoted by Yk = [yk1, yk2,…,ykj,…,xkJ], (k = 1,2,…,N) and the desired output is dk = [dk1, dk2,…,dkj,…,dkJ], (k = 1,2,…,N).
When the input signal is training sample Xk, the actual output of output neuron j is:
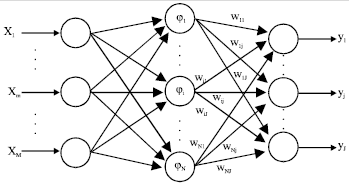 | |
| Fig. 2: | The network structure of RBFNN |
| (1) |
The basis function is Gaussian function as follow:
| (2) |
where, t is the centre of Gaussian function and σ is the variance. Therefore:
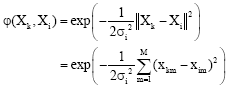 | (3) |
| • | The learning algorithm of RBFNN |
An entire-supervised algorithm of RBF neural network is proposed and in this way, the centre and other parameters of RBFNN are determined by supervised learning. There is one output in traffic prediction and the target function can be defined as follow:
| (4) |
where, ek is the error signal and
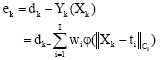 | (5) |
Therefore, the next step is to search the reasonable parameters ti, wi, ![]() and make the target function minimized. Gradient descent algorithm is often introduced to solve the optimization problem above and the specific calculation is shown as follow:
and make the target function minimized. Gradient descent algorithm is often introduced to solve the optimization problem above and the specific calculation is shown as follow:
The weights of output layer wi:
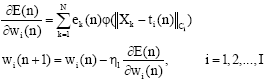 | (6) |
The centre of RBF hidden layer ti:
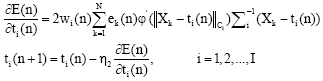 | (7) |
The extension of RBF hidden layer ![]() :
:
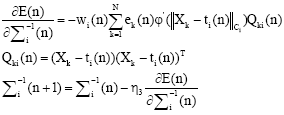 | (8) |
where, η1, η2, η3 denote the different learning rate, respectively.
The routing decision strategy: In routing decision stage, Mobile Agent (MA) is used to collect and exchange the information of satellite network (Zhu et al., 2010). MA is classified into forward agent and backward agent. The main idea of the routing strategy is that forward agents produced by satellites move among satellites. When forward agents arrive at destination satellite, they died and backward agents are produced. Afterwards, backward agents move along the same path but in the opposite direction, estimate path cost, finally update routing tables of the visited satellites. Forward agent is responsible for network exploration and information collection, while backward agent inherits the routing information of the forward agent and updates routing and pheromone table (Rahmatizadeh et al., 2009).
Informally, the behavior of TPDRA can be summarized as follows:
| • | From each satellite nodes s, mobile agents are generated towards specific destination nodes d at regular intervals. These agents are called forward agents because they are moving from source to destination and are indicated with |
| • | Each forward agent is a random experiment and it collects the non-local routing information about paths and traffic. Forward agents simulate data packets moving hop-by-hop from source node towards destination node. They have the same priority queues with data packets. Forward agents explore the satellite network concurrently, independently and asynchronously. Forward agents travel from a node to an adjacent one towards their destination. At each intermediate node, they use a stochastic decision policy to select the next hop. While moving, the forward agents collect information about the traveling time and the node identifiers along the paths they traveled |
| • | Once arrived at destination, the forward agent dies and a backward agent |
| • | When backward agent returns to the source node, it is removed from the network. Every mobile agent has a maximum time-to-live (TTL). If the mobile agent exceeds the TTL, it will also be destroyed |
| • | Data packets are routed according to a stochastic decision policy based on the information contained in the data-routing tables. These tables are derived from the pheromone tables which are used to route the mobile agents. At the same time, the pheromone tables are judged and modified by mobile agents. Only the best paths are stored in the data-routing tables which guarantee the transmission performance of data packets |
Data structures maintained at the satellite nodes: The performance of the routing policy is related to the information maintained at the network nodes. In TPDRA, each satellite node k comprises of five components including Pheromone matrix Tk, Data-routing table Rk, Link queues Lk and Statistical parametric model Mk.
Pheromone matrix Tk: is organized similarly to the routing tables in distance-vector algorithms, its entries are the goodness of choosing neighbor nodes as the next hop toward destinations. In other words, tnd represents the probability of link (k, n) to route data packets toward destination d. The tnd values are in the interval [0,1] and sum up to 1 along each destination column:
| (9) |
N is the number of nodes in satellite networks.
Data-routing table Rk is the routing table used to transmit data packets. Rk is a stochastic matrix and has the same structure as Tk. The entries of Rk are obtained by an exponential transformation and re-normalization to 1 of the corresponding entries of Tk. Data packets are probabilistically spread over the neighbors according to a stochastic policy which depends on the values of the stochastic matrix Rk.
Link queues Lk are data structures in a node. The status of the local link queues are a snapshot of what is going on at the precise time while Tk represents a long-term experience accumulated by the mobile agents of the network.
Prediction traffic Pk is data structure which records the predicted traffic from the earth. The entries of Pk are acquired from RBFNN and decides the future status of satellite nodes along with link queues Lk.
Statistical parametric model Mk is a vector of N-1data structures ![]() represent the sample mean and the variance of the traveling time to reach destination d from the current node, while Wd is the best traveling time over the window of the last w observations.
represent the sample mean and the variance of the traveling time to reach destination d from the current node, while Wd is the best traveling time over the window of the last w observations.
Forward agent behavior: At regular intervals Δt, forward agent Fs→d is launched at node s toward a destination node d aimed at discovering a feasible, low-cost path from s to d. Forward agent shares the same queues as data packets. The destination d is chosen with a probability pd:
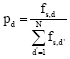 | (10) |
where, fs,d is the number of packets bounded for d that so far have passed by s.
While traveling toward their destination nodes, forward agent keeps a private memory H which is comprised of two lists. The list
maintains the ordered set of the nodes visited so far and the list
holds the values of the traveling times experienced by the forward agent.
At each intermediate node k, forward agent choose its next hop with the following way: If ![]() all the neighbors have been visited by the forward agent, then it chooses the next hop in a random way, but excluding the node from which forward agent arrived.
all the neighbors have been visited by the forward agent, then it chooses the next hop in a random way, but excluding the node from which forward agent arrived.
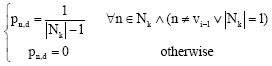 | (11) |
Otherwise, the forward agent applies a stochastic decision policy as follow:
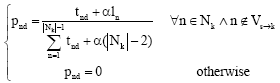 | (12) |
The value αε[0,1] weighs the relative importance of the heuristic correction with respect to the pheromone values.
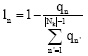 | (13) |
Here, In∈[0,1] is based on the status of the local link queues Lk and normalized by qn, qn is terms of packets waiting to be sent from node k to its neighbor n.
Backward agent behavior: Once the destination is reached, the forward agent Fs→d is terminated and the backward agent Bs→d is created, Bd→s contains all the information in the Fs→d and follows the identical path in the reverse direction but, being priority now, does not wait in queues. At each node on the return path, the Bd→s updates all the data structures.
Updating of the local models: Mk is updated consulting the list ![]() of the traveling time experienced by the forward agent while traveling from k to d. Equation 6 is used to update the values for μd and
of the traveling time experienced by the forward agent while traveling from k to d. Equation 6 is used to update the values for μd and ![]()
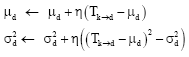 | (14) |
| (15) |
The factor η weights the number of most recent samples that will really affect the average.
Evaluation of the path: After updating the local traffic model Mk, the path visited by the forward agent must be evaluated. The concrete way is as follows:
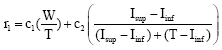 | (16) |
where, r1 is the reinforcement factor, W is the best traveling time experienced by the forward agent over the last observation window of size w samples. On the other hand, Isup and Iinf are estimates of the upper limit and the lower limit of μ in a certain of confidence interval. The coefficients c1 and c2 weigh the goodness and stability of the traveling time T.
Revising the reinforcement factor: R1 reflects the current state of satellite node and it has to be revised. When satellite node moves from low traffic region to high one, it is idle because the number of data packets is small at first. Therefore the value of r1 is large and it means the routing decision policy encourages data transmission to this node. But in fact, the traffic of this satellite node will increase in little time and the thoughtless decision may lead to congestion. Here the reinforcement factor r is improved by prediction traffic Pk.
Suppose that the prediction interval is Δt and ![]() is the predicted traffic in time t+Δt. Let Q and q(t) denotes the queue length and the queue occupancy at time t. The ISL capacity is C , the average packet size is davg and the size of buffer is B. Then the congest degree ξ(t) of satellite node is defined as follow:
is the predicted traffic in time t+Δt. Let Q and q(t) denotes the queue length and the queue occupancy at time t. The ISL capacity is C , the average packet size is davg and the size of buffer is B. Then the congest degree ξ(t) of satellite node is defined as follow:
| (17) |
ξ(t) shows the future state of satellite node and the revised factor γ is converted from ξ(t):
| (18) |
where, a is the slope parameter.
Then the final reinforcement factor r is calculated as follow:
| (19) |
Updating of the pheromone table: After getting the reinforcement value r, the pheromone table Tk is updated as follow:
| (20) |
tf,d represents the probability of choosing neighbor f when destination is d. All the probabilities sum up to 1 for the same destination d, so the probabilities tnd receive a negative reinforcement implicitly by normalization.
| (21) |
Updating of the data-routing table: The data-routing table Rk is updated after every update in the pheromone table. Data packets are routed according to a stochastic policy whose parameters are the entries of the data-routing table. The entries of Rk are defined as the result of an exponential transformation of those of the pheromone table. The transformation increases the impression of the high probability.
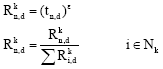 | (22) |
SIMULATION AND RESULTS
Here, Iridium satellite constellation is introduced to evaluate the performance of routing algorithms. There are 66 satellites distributed in 6 orbits at a height of approximately 781 km. Satellites communicate with neighboring satellites via inter-satellite links. Each satellite has four inter-satellite links: two to neighbors in the same orbital plane and two to satellites in neighboring planes to either side.
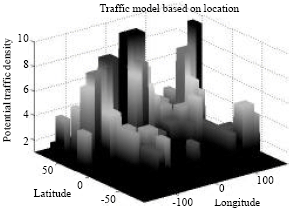 | |
| Fig. 3: | The potential traffic density of earth surface |
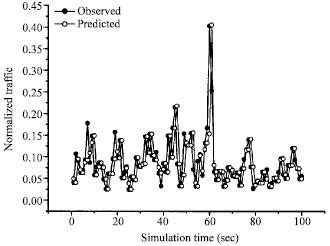 | |
| Fig. 4: | The prediction performance of TPDRA |
The potential traffic density is shown in Fig. 3 and the earth surface is divided into 288 grids by longitude 15° and latitude 15°. Every grid has traffic weighting according to the economy development of the area and ranges from 1 to 10. Other simulation parameters of algorithms are set as follow: α = 0.3, η = 0.2, c1 = 0.7, c2 = 0.3, a = 1. Ant Colony Optimization (ACO) in literature 8 (Hongbin et al., 2009) and TPDRA are compared in the simulation.
Figure 4 is the prediction performance of TPDRA and Fig. 5 is the comparison of TPDRA and fractional auto-regressive integrated moving average model (FARIMA) in literatue 9 (Ming et al., 2009). Figure 4 shows that the traffic prediction of TPDRA is accurate and timely which reflects the changing network flow. Figure 5 shows that the prediction performance of TPDRA is better. This is because the solution space of hidden layer is built based on Radial Basis Function and the input vector is transformed according to hidden layer.
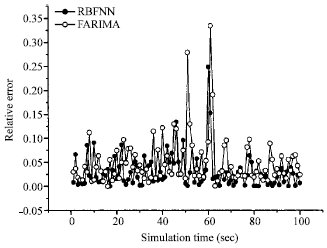 | |
| Fig. 5: | The prediction error comparison of RBFNN and FARIMA |
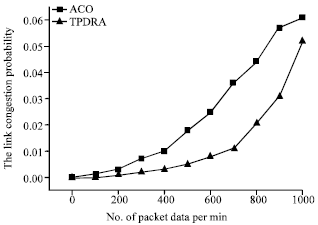 | |
| Fig. 6: | The link congestion probability of satellite node |
The input data with low dimensionality is converted to the high dimensionality space and the nonlinear separated problem in low dimensionality space is solved in high dimensionality space.
Figure 6 is the link congestion probability of satellite node in ACO and TPDRA. The potential traffic density is heterogeneous in the earth surface and when satellites move from the low traffic region to the high one, the congestion probability of satellite links increases due to the accessorial data packets from the terrestrial. Compared with ACO, traffic prediction which is the important component of TPDRA revises the routing strategy and avoid packets transmission to the impending congested satellite nodes.
Figure 7 shows the average packet delay of two algorithms. Facing high degree of burst traffic, the packet delay of ACO increases rapidly and the link of satellite nodes is jammed until mobile agents find out. By comparison, TPDRA makes the satellite node deal with the burst traffic wholeheartedly through restraining the data transmission from neighboring satellites.
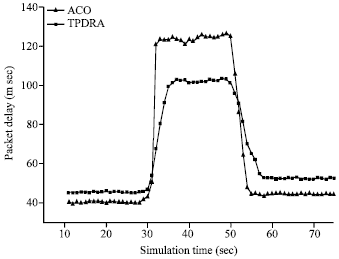 | |
| Fig. 7: | The packet delay of ACO and TPDRA |
Therefore, TPDRA has a reinforced robustness performance encountering the unexpected situation.
CONCLUSION
In this study, we introduced a adaptively distributed routing algorithm with traffic prediction TPDRA for LEO satellite networks. TPDRA uses traffic prediction module and routing decision module. The former predicts the upcoming traffic from the terrestrial and revises the routing decision. The latter uses MA to collect the network information and the decision strategy is not only depending on the current state of satellite networks, but also related to the future state of satellite nodes. Because of the traffic prediction and dynamic data balance between satellite nodes, TPDRA improves the robustness of satellite networks. By simulations, the agreeable results also demonstrate that TPDRA outperforms other algorithms. To concluded, TPDRA is promising in LEO satellite networks.
ACKNOWLEDGMENT
This research is supported by the National Science and Technology Specific Project of China (2009ZX03005).
REFERENCES
- Darnopykh, V.V., 2010. Application of unified methodical approach to online planning of target operation of satellite monitoring and communication systems. J. Comput. Syst. Sci. Int., 49: 115-134.
CrossRef - Uzunalioglu, H., I.F. Akyildiz and M.D. Bender, 2000. A routing algorithm for LEO satellite networks with dynamic connectivity. J. Wireless Networks, 6: 181-190.
CrossRef - Wood, L., A. Clerget and I. Andrikopoulos, G. Pavlou and W. Dabbous, 2001. IP routing issues in satellite constellation networks. Int. J. Satellite Commun., 19: 69-92.
CrossRef - Ekici, E., L.F. Akyildiz and M.D. Bender, 2001. A distributed routing algorithm for datagram traffic in LEO satellite networks. IEEE/ACM Trans. Network., 9: 137-147.
CrossRef - Kim, B.W., S.L. Min, H.S. Yang and C.S. Kim, 2001. A predictive call admission control scheme for low Earth orbit satellite networks. J. IEEE Trans. Vehicular Technol., 49: 2320-2335.
CrossRef - Lee, C.C. and C.Y. Shih, 2007. Time series prediction using robust radial basis function with two-stage learning rule. Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence, (ICTAI`07), Patras, Greece, pp: 382-387.
CrossRef - Zhu, C.Y., Y.Y. Du and P. Li, 2010. A routing-based dynamic workflow. Inform. Technol. J., 9: 561-568.
CrossRef - Rahmatizadeh, S., H. Shah-Hosseini and H. Torkaman, 2009. The ant-bee routing algorithm: A new agent based nature-inspired routing algorithm. J. Applied Sci., 9: 983-987.
CrossRefDirect Link








