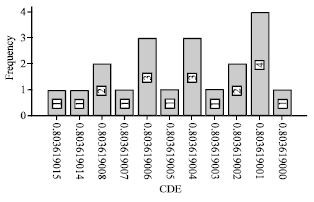
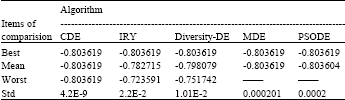
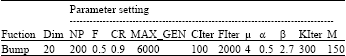Research Article
Chaotic Differential Evolution Algorithm for Solving Constrained Optimization Problems
Zhengzhou Institute of Aeronautical Industry Management, Countrs, China
Xiang Wang
Zhengzhou Institute of Aeronautical Industry Management, Countrs, China