Research Article
The Selection of Optimal Ordering Strategy for Retailer with Multi Suppliers
School of Managemen, Harbin University of Commerce, Harbin, China
Yi Liu
School of Managemen, Harbin University of Commerce, Harbin, China
Recently, more and more products update faster, product lifecycle gradually shortened, with the progress of technology and the strengthening of market competition. Such as: electronic products, personal computer and information technology products, etc. The produces with short lifecycle have the properties of intense timeliness, great fluctuation demand, less residual value and a complex nonlinear relation with external environment. Supply and requisitioning parties in supply chain are facing more and more severe challenges.
Based on the short lifecycle of product, retailer’s ordering strategy research has aroused wide discusses. Donohue studied the ordering strategy of fashionable products with multiple production opportunities, the conclusion is that the two stage order strategies can better adapt to the market demand fluctuation and improve supply chain performance (Donohue, 2000). Based on the short lifecycle of product warranty, considering the plan period may not be integer times of the most optimal ordering cycle, Chen etc. studied the optimal two stage order strategies of metamorphic products that has shelf life constraints and plan period modified in a general sense (Chen et al., 2009). Cai et al. (2010) considered the two-echelon supply chain in a uncertain demand environment that has single season sale goods, analyzed the game model between single supplier and multi retailers. Research shows that when retailers have second order chance, suppliers can to improve its own profit level by optimizing. Based on the characteristics of short lifecycle products, Xu and Nie (2009) studied order decision model of a two-echelon supply chain that the core enterprise is retailers. Choi (2007) studied the two stage order issue when the sales price unknown and there are two freight modes. Based two stage order strategy, Weng discussed the new coordination strategy on short lifecycle products two-echelon supply chain composed by single manufacturer and single retailer. For the first time, from the angle of the manufacturer, the model considered the manufacture’s willingness to its second producing, in order to meet retailer’s second emergency order (Weng, 2004). Based on the situation of retailer emergency order, Zhou and Wang (2009) constructed the system profit function of the newsboy products that its return products can repeat sale, having second order chance or not. Then compared the two system profit functions to prove the validity of the two stage order strategy (Weng, 2004). Miltenburg studied the two stage order strategy of multi seasonal short lifecycle produces, gave respectively profit model in which the two stage production cost are equal and not equal and discussed the algorithm detailed (Miltenburg and Pong, 2007). Supply chain’s coordination with short lifecycle product, composed by single manufacturer and multi retailers, has been considered by Shengdong Wang and Zhou (2009) who deemed that for the conflict of two stage order strategy, is the unit quantity discount coordination strategy. Ding et al. (2004) supposed that improving returns price or unsalable subsidies can increase retailer’s expected profits and total order quantity which more tend to the first stage order strategy rather than the second stage order strategy.
Chen and Li (2008) studied on the basis of the given condition of the second order stage how retailer determines whether adjust the second order quantity which depend expected profits brought by updated demand information. Lan and Lau (1997) pointed out that in either case, when the goods have higher profit margins, the manufacturer has less enthusiasm of the second stage order; while, more enthusiasm when lower profit margins. Gurnani and Tang (1999) assumed the uncertain cost of the second stage order which have probability of high and low costs, considered separately two stage order strategy under the situations of incomplete information asymmetric and completely information symmetric, proved that the better information symmetry the less total order quantity. Choi et al. (2003) studied two stage order strategy under the condition of the second stage order cost is a random variable, analyzed the change of the service level caused by different costs. Based on retailer’s order strategy of short lifecycle products many literatures focused on the two stage order strategy. But these studies discussed the theme that single retailer or multi retailers order from single suppler. And the impact to the retail’s profit aroused by order cost and order quantity adjustment was not considered.
Meanwhile, for the issue of the retailer orders from multi suppler, many scholars have made the corresponding research. In the background of downstream retailer mighty, Wang and Lu (2008) studied order strategy of supply chain composed by multi suppliers and single retailer, discussed profit differences of order strategy between centralized decision-making system and decentralized decision-making system. Based on BOM table relationship, Wan and Huang (2010) constructed two suppliers-single manufacturer supply chain model for optimal supply chain cost, under the constraints of normal distribution demand and given service level which decides manufacturer’s order lead time and order quantity when manufacturer ordering from suppliers, respectively. Due to the particularity of short lifecycle production, the retailer often adopts ordering from multi suppliers in order to meet the market demand effectively. But there are little studies discussing about order strategy of short lifecycle production facing multi suppliers.
Considered the retailer’s adjustment of order quantity and the accumulation of order cost, whether two stage order strategy of retailer is still better than one stage order strategy? For this problem, this study establish profits analysis model by determining selection conditions for suppliers and the optimal order quantity of retailer according to every supply’s wholesale prices and his production capacity. Compared and analyzed the influence differences to the retailer’s profit between the two of order strategy, trying to find the better order strategy to help retailer obtaining more profit.
DESCRIPTION AND MODEL ESTABLISHMENT
Description: Considered the trade between multi suppliers and one retailer (assume the number of suppliers is n), assume that all production of suppliers can be substituted and be sold in market by downstream retailer only. Then, the retailer who is considering the order strategy facing the problem: which strategy should be adopted? One stage order strategy or two stage order strategy? How to obtain more profit?
Assume order cycle is T. Wholesale prices wi and production capacity gi (1≤i≤n) of supplier I (1≤i≤n) are constant. Retailer’s order demand G (wi) for supplier is negative with wi, order cost per time is Ci which usually takes small percentage of the total cost. Every good sell price p. At the end of sale cycle, if there are still market demands are not met, retailer’s shortage costs v; corresponding, if there are still unsold products, every unsold good sell at price of s. In this study, the actual needs of customers D is a random variable, expected value is μ, variance is σ, probability density function is f (x) and distribution function is f (x). In the circumstance of multi suppliers, usually, to the retailer, every supplier supplies the wholesale prices are completely the same. This led to retailers for each supplier ordering demand and order quantity will not all be identical. Each supplier's production ability is limited, retailer can not always order all the production from the supplier who supplied the lowest wholesale prices, the retailer must consider to order from two or more than two suppliers.
Model establishment and analysis
Retailer profit analysis under one stage order strategy: Based on the description, we first make the following assumption:
| • | Asumption 1: s<w1≤w2≤....≤wn<p |
| • | Asumption 2: There are at least a group (I, j), let wi≠wj, 1≤i, j≤n |
| • | Asumption 3: In order to get optimal profit, retailer chooses to order from the supplier who supplies the lowest wholesale price |
| • | Asumption 4: g1<G (w1) |
Assumptions above rank the suppliers according to the wholesale price from low to high and these suppliers’ wholesale prices are completely the same. According assumption 3, retailer first chooses the supplier 1 who supplies the lowest wholesale price and then, the supplier 2 and so on. Retailer will keep choosing till his order demand is satisfied. Assumption 4 ensures that the retailer must consider to ordering from two or more than two suppliers, this conform to the study situation that one retailer orders from multi suppliers.
Theorem 1: Facing multi suppliers 1≤i≤m≤n, whose wholesale price s<w1≤w2≤....≤wm≤....≤wn<p, production capacity gi (1≤i≤n), when single retailer adopt one stage order strategy, the supplier m who has been chosen satisfies:
or
retailer’s optimal order quantity is:
Proof: Derive from assumption 3 and assumption 4, retailer order from the supplier who has lowest wholesale price as many as possible, i.e., supplier 1. In order to obtain retailer’s profit maximum, we have:
This function consist of five parts: sales revenue, goods purchase cost, possible disposal value caused by excess inventory, possible shortage costs caused by supply shortage and order cost of retailer ordering from supplier 1 per time.
Based on assumption 4, this maximization problem has the solution:
After ordering from supplier 1, retailer still needs to order from other suppliers.
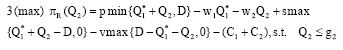 |
Considering existing stock Q1* and wholesale price of supplier 2 is more competitive, retailer choose to order from supplier 2. In order to obtain retailer’s profit maximum, we have:
This maximization problem has the solution:
Based on discussion above, for supplier 2, order strategy of retailer has three choices:
| • | (1) Not order, Q2* = 0. If and only if Q1* >G (w1)+ G (w2). Now Q1* = g1, equivalent to g1>G (w1)+ G (w2) |
| • | (2) Order, Q2*≠0. But production capacity of supplier 2 is higher than order quantity of retailer. If and only if [G (w1)+G (w2)]-Q1*<g2. Now, Q1* = g1, equivalent to Q2* = [G (w1)+G (w2)]-g1, g1+g2>G (w1)+G (w2)>g1 |
| • | (3) Order, Q2* ≠ 0, Production capacity of supplier 2 is equal to order quantity of retailer. If and only if [G (w1)+G (w2)]-Q1* = g2. Now, Q1* = g1, Q2* = g2, equivalent to g1+g2≤G (w1)+G (w2) |
Considering existing stock Q1*+Q2*, retailer considers whether order from supplier 3. Similar:
| • | If, Q2* = 0, Q1* = g1 retailer has not order from supplier 2, i.e., g1> G (w1)+G (w2)> g1, so retailer will not order from supplier 3, or even to order from supplier I (4≤i≤n) |
| • | If Q2* = [G (w1)+G (w2)]-g1, Q1* = g1, retailer ordered to supplier 2 and production capacity of supplier 2 is higher than order quantity of retailer, i.e., g1+g2>G (w1)+G (w2)>g1, at this time retailer order quantity has met the market demand , retailer will not order from supplier 3, or even to order from supplier I (4≤i≤n) |
| • | If Q2* = g2, Q1* = g1, retailer ordered to supplier 2 and production capacity of supplier 2 is equal to order quantity of retailer, i.e., g1+g2≤G (w1)+G (w2), at this time, retailer still needs to order from supplier 3 |
Similar, this maximization problem has the solution:
Based on discussion above, we have corollary as following:
Retailer chooses m numbers of suppliers from n numbers, assume m (2<m≤n), the order quantity is (Q1*, Q2*,......,Qm*). We have:
After ordering to supplier j, the condition that retailer still needs to order from supplier (j+1) is:
According above, the supplier m who has been chosen satisfies:
or
Each supplier’s optimal order quantity Qi* should satisfy: 1≤i≤m-1, Qi* = gi, m<i≤n, Qi* = 0;
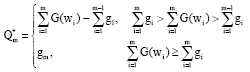 |
From this it is clear that the optimal order quantity of retailer is ![]() , i.e.,
, i.e.,
Hence, theorem 1 established.
Retailer should try to select suppliers whose wholesale price and production capacity are competitive as much as possible. When order demand has not been satisfied, retailer order from top m-1 numbers of suppliers according their production capacity, i.e., Qi* = gi; meanwhile, retailers will not be ordering unlimited. For supplier m, retailer will not make the order quantity equal to its production capacity, but rather ordering that part of quantity that just meet the demand, at the request of the market demand.
From theorem 1, we derive the following:
In random market demand D, derive expected value of function above, get expected profit value of retailer:
Considering ![]() and
and ![]() , simplify the function above:
, simplify the function above:
 | |
| Fig. 1: | Two stage order strategy |
Retailer profit analysis under two stage order strategy: Two stage order strategy means that at the beginning of order cycle supplier quote the wholesale price to retailer and retailer determine the order quantity according the wholesale price and market demand forecasting; and then, at the end of order cycle, supplier quote to retailer for the second time according self production condition and market demand situation; at this time, these two wholesale price are different and retailer adjust order quantity according the new quote price of supplier and more accuracy market demand information. If market demand is more than the first stage order quantity, retailer will replenish at the second stage wholesale price; contrarily, if market demand is less than the first stage order quantity, retailer will return the excess at the second stage wholesale price (Fig. 1).
Because gi is a constant, supplier whose production ability is limited hope retailer ordering as early as possible, in order to recover funds and arrange producing reasonable. But, considered the trade between multi suppliers and one retailer, whether two stage order strategy is good for improving retailer’s profit level.
According process of two stage order strategy, we make the following assumption:
| • | Asumption 5: The wholesale price of supplier at the beginning of order cycle t is wi and at the end of order cycle T is wi |
| • | Asumption 6: At t time retailer order Qi from each supplier and at T time retailer adjust each order quantity ΔQi, at the end the optimal order quantity Qi* |
For simplifying issue, we assume that at T time the supplier’s wholesale are same between the two order strategies. Assumption 6 gives expression to characteristics of two stage order strategy, retailer ordered at the beginning of order cycle and as the change of wholesale price of supplier, retailer adjust the order quantity, Qi ≠ 0,ΔQi ≠ 0.
Regardless one stage order strategy or two stage order strategy, at T time the supplier’s wholesale is wi. So, supplier selection and each supplier’s optimal order quantity Qi* are same as one stage order strategy (Chen, 2005). Qi* = Qi*, then, the optimal order quantity of retailer.
At order cycle T time, considering the corresponding order cost caused by adjustment of retailer’s order quantity in two stage order strategy, the profit function of retailer is following:
i.e.,:
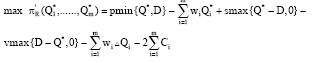 |
In random market demand D, derive expected value of function above, get expected profit value of retailer:
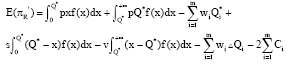 |
Simplify the function above:
We can derive that:
profit of retailer decline.
From what has been discussed above, we may draw the conclusion that:
Adopting two stage order strategy, retailer adjust order quantity makes expected profit value of retailer decline. Specially, if retailer adjusts order quantity a lot, the value of ΔQi increases large, the loss of retailer’s profit will be a lot. At the same time, although order cost per time of retailer usually takes small percentage of the total cost, every time order one more time, the order cost of retailer ![]() will bring the profit loss that can not be ignored to retailer, in condition of ordering from multi suppliers.
will bring the profit loss that can not be ignored to retailer, in condition of ordering from multi suppliers.
Therefore, considered the trade between multi suppliers and one retailer, although two stage order strategy is good for suppliers, this strategy will bring profit loss that can not be ignored to single retailer.
Analyzing of retailer’s order strategy selection: According analysis above, two stage order strategy is not always good for retailer. Then, should the single retailer adopt one stage order strategy facing multi suppliers and their wholesale price.
Theorem 2: At order cycle T time, facing multi suppliers 1≤i≤m≤n, the wholesale price s<w1≤w2≤. ..... ≤wm≤ ..... ≤wn<p, production capacity gi (1≤i≤n), retailer should adopt one stage order strategy in order to ensure maximum profits.
Proof: Based on assumption 5, at order cycle T time, assume retailer choose two stage order strategy, expected profit value of retailer is E (πR) = E (πR). Considering retailer seeks to maximize the benefits, let E (πR) = E (πR), we can derive:
Then, the function above has unique solution Qi = 0. Considering Qi* = Qi* and
at order cycle T time, facing multi suppliers 1≤i≤m≤n, the wholesale price s<w1≤w2≤......≤wm≤.....≤wn<p, production capacity gi (1≤i≤n), retailer reduce profit loss caused by order cost ensure maximum profits. Obviously, it is the order quantity with the first order stage that should not be adjusted, from the aspect from the retailer. So, we can draw a conclusion that retailer will adopt one stage order strategy rather than two stage order strategy and the optimal order quantity must be defined from this strategy.
Hence, theorem 2 established.
SIMULATION
Chopra and Meindl (2008) considered that demand is a function that decreasing on price changing expressed by multiplication. Assume that the relation between order demand G (wi) and production wholesale price wi is ![]() . One of the coefficients of price sensitivity a indicate that the variations in retail demand when the wholesale price decrease (or increase) in one unit; the other coefficients of price sensitivity b indicate that intensity of retailer demand reflection caused by variations in wholesale price.
. One of the coefficients of price sensitivity a indicate that the variations in retail demand when the wholesale price decrease (or increase) in one unit; the other coefficients of price sensitivity b indicate that intensity of retailer demand reflection caused by variations in wholesale price.
Assume the number of upstream suppliers is n = 10; the wholesale prices are w1 = 10, w2 = 20,...,w10 = 100 and production capacities are g1 = 1000, g2 = 900,...,g10 = 100; the coefficients of price sensitivity a = 2000, b =2, therefore order demand function is ![]() , thereinto,i = 1,2,.....,10.
, thereinto,i = 1,2,.....,10.
 | |
| Fig. 2: | Retailer’s profit under the two kinds of ordering strategy |
| Table 1: | Supplier selection and optimal order quantity for retailer |
| Table 2: | Retailer’s profits from one stage order strategy and two stage order strategy |
Order costs of retailer to each supplier are C1 = 1, C2 = 2, ..., C10 = 10. Other parameter is set: p = 110, v = 90, s = 20. Through the simulation based on matlab environment on computer, retailer selected suppliers to whom ordered, determined optimal order quantity, adopted order strategies (one stage order strategy or two stage order strategy.) and compared the profit of two kinds of strategy (Table 1, 2).
Therefore, through computer simulation, facing 10 suppliers, the wholesale price wi = 10, w2 = 20,..., w10 = 100, production capacity g1 = 1000, g2 = 900,...,g10 = 100, retailer order to the first 5 suppliers who provided lowest wholesale price, i.e., m = 5. With wholesale prices rising, retailers reduce the optimal order quantity. The optimal order quantities of first 4 suppliers are just, respectively equal to each supplier’s production capacity. However, for supplier 5, retailer do not make the order quantity equal to its production capacity, but rather ordering that part of quantity that just meet the demand, at the request of the market demand. See Table 1. This simulation result supports theorem 1. Meanwhile, in short lifecycle product market random demand, for the profit level of single retailer, one stage order strategy is superior to two stage order strategy. See Table 2. This simulation result supports theorem 2.
The simulation above just discussed the situation that there are only 10 suppliers joining the trade. Furthermore, assume n = 100. Through the simulation based on matlab environment on computer, profit variation of retailer for two kinds of order strategy is following (Fig. 2).
According Fig. 2, there are two layers: the top layer stands for the profit on the one stage order strategy and the bottom layer stands for the profit on the two stage order strategy.
| • | When production capacity of suppliers is constant, retailer’s profit increased. However, along with the increase of the wholesale price (that means new suppliers joined), retailer’s profit growth rate transitioned into slow from rapid. When supplier number had grown to a certain degree, retailer’s profit stopped increasing. It is that along with more and more suppliers joined the trade, retailer’s profit grew, forming economies of scale. However, when too many suppliers joined, the profit growth slowed and eventually stops growing |
| • | When the number of suppliers is not a lot, the profit caused by the two kinds of order strategy are nearly same. However, along with facing more and more suppliers, the situation of retailer profit has changed. The profit when retailer adopted one stage order strategy much higher than two stage order strategy |
For short lifecycle product, the study of multi suppliers will be very helpful to the theory and practice. Analyzed order strategy of single retailer facing multi suppliers in short lifecycle product market random demand and compared the influence of the two kind of order strategy to the retailer's profits. Assumed that each supplier has certain production capacity and different wholesale price, retailer has to pay order cost to every supplier every order stage. Considering the suppliers' wholesale prices and their individual production capacity, retailer would select suppliers with the optimal order quantity. Through analyzing and comparing the influence of the two kind of order strategy to the retailer's profits and computer simulation analysis, there reached the conclusion: In short lifecycle product market random demand, although two stage order strategy is good for suppliers on recovering funds and arranging producing reasonable, this strategy will bring profit loss that can not be ignored to single retailer, considering the retailer’s adjustment of order quantity and the accumulation of order cost. On the contrary, retailer should adopt one stage order strategy in order to pursue maximum profits.
The innovation of this study lies in that for order strategy of short lifecycle product, most studies supposed that one stage order strategy might be superior. However, based on the study of multi suppliers, through comparing and analyzing profit function of retailer, we found that two stage order strategy is not superior to one stage order strategy in the reason of order cost increases caused by order stage increases.