Research Article
Semi Automatic Method for String Matching
Dr. M.G.R. University, Chennai, Tamilnadu, India
S. K. Srivatsa
St. Joseph Engineering College, Chennai, Tamilnadu, India
Researchers have investigated the problem of identifying duplicate objects under several monikers, including record linkage, merge-purge, duplicate detection, database hardening, identity uncertainty, co-reference resolution and name matching. Such diversity reflects research in several areas: statistics, databases, digital libraries, natural language processing and data mining. Our research explores approaches to the name-matching problem that improves accuracy. Particularly, we employ methods that adapt to a specific domain by combining multiple string similarity methods (Rajesh and Srivatsa, 2009) that capture different notions of similarity. Because an estimate of similarity between strings can vary significantly depending on the domain and specific field under consideration, traditional similarity measures may fail to estimate string similarity correctly. At the token level, certain words can be informative when comparing two strings for equivalence, while others are ignorable. For example, ignoring the substring Street may be acceptable when comparing addresses, but not when comparing names of people (e.g., Nick Street) or newspapers (e.g., Wall Street Journal). At the character level, certain characters can be consistently replaced by others or omitted when syntactic variations are due to systematic typographical or OCR errors. Thus, accurate similarity computations (Mansi and Alnihoud, 2010) require adapting string similarity metrics for each field of the database with respect to the particular data domain.
LITERATURE SURVEY
We examine a few effective and widely used metrics for measuring similarity.
Edit distance: An important class of such metrics is edit distances. Here, the distance between strings s and t is the cost of the best sequence of edit operations that converts s to t. Edit Operations are listed as follows Eq. 1:
| • | Copy character from string1 over to string2 (cost 0) |
| • | Delete a character in string1 (cost 1) |
| • | Insert a character in string2 (cost 1) |
| • | Substitute one character for another (cost 1) |
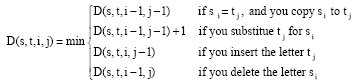 | (1) |
The simple unit-cost metric just described is usually called Levenshtein distance (Hernandez and Stolfo, 1995; Joachims, 1999). There are many extensions to the Levenshtein distance function typically these alter the d(i,j) function, but further extensions can be made for instance, the Needleman-Wunch distance for which Levenshtein is equivalent if the gap distance is 1. The Levenshtein distance is calculated below (Table 1) for the term sam chapman and sam john chapman, the final distance is given by the bottom right cell, i.e., 5. This score indicates that only 5 edit cost operations are required to match the strings (for example, insertion of the john characters, although a number of other routes can be traversed instead).
| Table 1: | Computing levenstein distance |
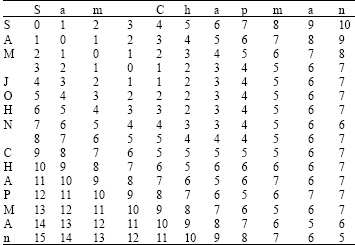 | |
We can evaluate this recursive definition efficiently using dynamic programming techniques. Specifically, for a fixed s and t, we can store the D(s, t, i, j) values in a matrix that is filled in a particular order. The total computational effort for D(s, t, |s|, |t|), the edit distance between s and t, is thus approximately O(|s||t|). Edit distance metrics are widely used not only for text processing but also for biological sequence alignment1and many variations are possible.
Affine gap method: Needleman and Wunsch (1970) extended the model to allow contiguous sequences of mismatched characters, or gaps, in the alignment of two strings and described a general dynamic programming method for computing edit distance. Most commonly the gap penalty is calculated using the affine model: cost(g) = s + e x l, where s is the cost of opening a gap, e is the cost of extending a gap and l is the length of a gap in the alignment of two strings, assuming that all characters have a unit cost. Usually e is set to a value lower than s, thus decreasing the penalty for contiguous mismatched substrings. Since differences between duplicate records often arise because of abbreviations or whole-word insertions and deletions, this model produces a more sensitive similarity estimate than Levenshtein distance.
String distance with affine gaps between two strings of lengths l1 and l2 can be computed using a dynamic programming algorithm that constructs three matrices in O(l1l2) computational time. The following recurrences are used to construct the matrices, where c(xi, yj) denotes the cost of the edit operation that aligns ith character of string x to jth character of string y, while c(xi, 2) and c(2, yj) are insertion and deletion costs for the respective characters. Matrix M represents a minimum-cost string alignment that ends with matched characters, while matrices I and D represent alignments that end with a gap in one of the two strings (Eq. 2-5):
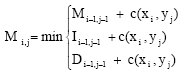 | (2) |
| (3) |
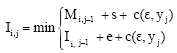 | (4) |
| (5) |
Needleman-Wunch distance or sellers algorithm: This approach is known by various names, Needleman-Wunch, Needleman-Wunch-Sellers, Sellers and the Improving Sellers algorithm. This is similar to the basic edit distance metric, Levenshtein distance; this adds an variable cost adjustment to the cost of a gap, i.e., insert/deletion, in the distance metric. So, the Levenshtein distance can simply be seen as the Needleman-Wunch distance with G = 1.
| • | D(i-1,j-1) + d(si,tj) //subst/copy |
| • | D(i,j) = min D(i-1,j)+G //insert |
| • | D(i,j-1)+G //delete |
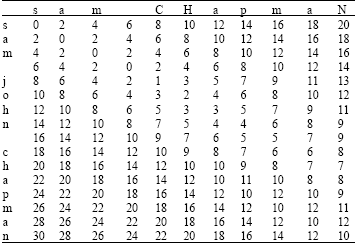
where, G = gap cost and d(c,d) is again an arbitrary distance function on characters (e.g., related to typographic frequencies, amino acid substitutability, etc.). The Needleman-Wunch distance is calculated below for the term sam chapman and sam john chapman, with the gap cost G set to 2 (Table 2). The final distance is given by the bottom right cell, i.e., 10. This score indicates that only 10 edit cost operations are required to match the strings (for example, insertion of the john characters, although a number of other routes can be traversed instead).
Smith-Waterman distance: Again similar to the to Levenshtein distance, this was developed to identify optimal alignments between related DNA and protein sequences. This has two main adjustable parameters a function for an alphabet mapping to cost values for substitutions and costs, (the d function). This also allows costs to be attributed to a gap G (insert or delete).
| Table 2: | Computing Needleman-Wunch distance |
 | |
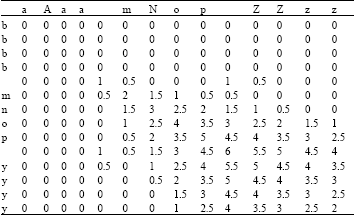
| Table 3: | Computing Smith-Waterman distance |
 | |
The final similarity distance is computed from the maximum value in the path where,
| • | 0 //start over |
| • | D(i-1,j-1) -d(si,tj) //subst/copy |
| • | D(i,j) = max D(i-1,j)-G //insert |
| • | D(i,j-1)-G //delete |
Distance is maximum over all i,j in table of D(i,j)
| • | G = 1 //example value for gap |
| • | d(c,c) = -2 //context dependent substitution cost |
| • | d(c,d) = +1 //context dependent substitution cost |
The Smith-Waterman distance is calculated below for the term aaaa mnop zzzz and bbbb mnop yyyy, with the gap cost G set to 0.5 (Table 3) and where d(c,c) = -2, d(b,c) = 1. The final distance is given by the highest valued cell, i.e., 6. This score indicates that the longest approximately matching string terminates in the cell with the highest value so the sequence mnop matches in both strings.
An extension of this technique was made by Gotoh in 1982 which also allows affine gaps to be taken into consideration.
 | |
| Fig. 1: | Computation of Jaro Metric |
This extension was incorporated into the better known Monge Elkan distance.
The Jaro metric and variants: Another effective similarity metric is the Jaro metric (Cook and Holder, 1994; Durbin et al., 1998; Baeza-Yates and Ribeiro-Neto, 1999) which is based on the number and order of common characters between two strings. 4-6 Given strings s = a1 aK and t = b1, bL, define a character ai in s to be in common with t iff there is a bj = ai in t such that i -≤j≤ i + H, where H = min(|s|,|t|)/2. Let be the characters in s that are common with t (in the same order they appear in s) and let be analogous. Then define a transposition for s', ![]() to be a position i such that ai = bi. Let Ts',
to be a position i such that ai = bi. Let Ts', ![]() be one-half the number of transpositions for
be one-half the number of transpositions for ![]() and t'. The Jaro metric for s and t is Eq. 6:
and t'. The Jaro metric for s and t is Eq. 6:
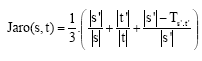 | (6) |
To better understand the intuition behind this metric, consider the matrix M in (Fig. 1), which compares the strings s = WILLLAIM and t = WILLIAM. The boxed entries are the main diagonal and M(i, j) = 1 if and only if the ith character of s equals the jth character of t. The Jaro metric is based on the number of characters in s that are in common with t. In terms of the matrix M of the figure, the ith character of s is in common with t if Mi,j = 1 for some entry (i, j) that is “sufficiently close” to M’s main diagonal, where sufficiently close means that |i![]() j| < min(|s|, |t|)/2 (shown in the matrix in bold). William Winkler proposed a variant of the Jaro metric that also uses the length P of the longest common prefix of s and t. Letting
j| < min(|s|, |t|)/2 (shown in the matrix in bold). William Winkler proposed a variant of the Jaro metric that also uses the length P of the longest common prefix of s and t. Letting ![]() = max(P, 4), we define Jaro-Winkler(s, t) = Jaro(s, t) + (P'/10) . (1
= max(P, 4), we define Jaro-Winkler(s, t) = Jaro(s, t) + (P'/10) . (1![]() Jaro(s, t)). This emphasizes matches in the first few characters. The Jaro and Jaro-Winkler metrics seem to be intended primarily for short strings (for example, personal first or last names).
Jaro(s, t)). This emphasizes matches in the first few characters. The Jaro and Jaro-Winkler metrics seem to be intended primarily for short strings (for example, personal first or last names).
Jaccard index: The Jaccard index, also known as the Jaccard similarity coefficient (originally coined coefficient de communauté by Paul Jaccard), is a statistic used for comparing the similarity and diversity of sample sets Eq. 7. The Jaccard coefficient measures similarity between sample sets and is defined as the size of the intersection divided by the size of the union of the sample sets:
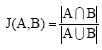 | (7) |
The Jaccard distance, which measures dissimilarity between sample sets, is complementary to the Jaccard coefficient and is obtained by subtracting the Jaccard coefficient from 1, or, equivalently, by dividing the difference of the sizes of the union and the intersection of two sets by the size of the union Eq. 8:
| (8) |
Tanimoto coefficient (extended Jaccard coefficient): Cosine similarity is a measure of similarity between two vectors of n dimensions by finding the angle between them, often used to compare documents in text mining. Given two vectors of attributes, A and B, the cosine similarity, θ, is represented using a dot product and magnitude as in Eq. 9:
| (9) |
For text matching, the attribute vectors A and B are usually the tf-idf vectors of the documents. Since the angle, θ, is in the range of [0,π], the resulting similarity will yield the value of ð as meaning exactly opposite, π/2 meaning independent, 0 meaning exactly the same, with in-between values indicating intermediate similarities or dissimilarities.
This cosine similarity metric may be extended such that it yields the Jaccard coefficient in the case of binary attributes. This is the Tanimoto coefficient, T(A,B), represented as in Eq. 10:
| (10) |
TF/IDF: In many situations, word order is unimportant. For instance, the strings Ray Mooney and Mooney, Ray are likely to be duplicates, even if they aren’t close in edit distance. In such cases, we might convert the strings s and t to token multi-sets (where each token is a word) and consider similarity metrics on these multi-sets. One simple and often effective token-based metric is Jaccard similarity. Between the word sets S and T, Jaccard similarity is simply (|![]() ∩T|)/(|S
∩T|)/(|S![]() T|). We can define term frequency-inverse document frequency (TF-IDF) (Robertson, 2004) or cosine similarity-which the information retrieval community widely uses (Baeza-Yates and Ribeiro-Neto, 1999) - as in Eq. 11:
T|). We can define term frequency-inverse document frequency (TF-IDF) (Robertson, 2004) or cosine similarity-which the information retrieval community widely uses (Baeza-Yates and Ribeiro-Neto, 1999) - as in Eq. 11:
| (11) |
where, Tfw, S is the frequency of word w in S, IDFw is the inverse of the fraction of names in the corpus that contain w, V’(w, S) = log(TFw,S + 1) . log(IDFw) and for name matching, you might collect the statistics used to compute IDFw from the complete corpus of names to be matched. TF-IDF distance is attractive in that it weights agreement on rare terms more heavily than agreement on more common terms. This means that Ray Mooney and Wray Mooney will be considered more similar than, say, Ray Mooney and Ray Charles.
Based on the discussions above we can come to a conclusion that no single method independently can provide optimum results. In this paper we propose a hybrid method which combines the affine gap method, a domain specific dictionary and TFIDF in a novel way to get the benefits of all the methods.
HYBRID STRING MATCHING PROCESS
We first tokenize the strings to be matched based on common delimiters like space, comma, semicolon, underscore etc and if there is a change in the case i.e., from lower case to upper case between successive letters of the string. If the strings are made up of just a single word then we compute the similarity between the strings using dictionary first. If they are synonyms then a match value of 1 is assigned to the pair. If they are not synonyms then the similarity is computed using the affine gap method and the match value between the pairs is then obtained. As in the literature, the match value between any pair of strings fall between 0 to1. Any string pair whose match value is greater than a pre specified threshold is taken as equivalent or matching.
If the strings are made up of multiple words then each word from the two strings are matched with one another using the above described method. And the matching word pairs between the two strings are obtained. Now the TFIDF value between the two strings is computed using this set of matched word pairs identified between the two strings. The strings are considered to be matching or equivalent if the TFIDF value of the two strings exceeds a predefined threshold. Thus instead of taking the set of words present in both the strings to compute the TFIDF we are taking the set of similar words as identified by the affine gap method or dictionary to compute the TFIDF.
The affine gap method ensures that words with spelling mistakes, acronyms, prefix and suffixes match properly. The dictionary ensures that synonyms are matched properly. And TFIDF ensures that words found rarely are given higher weightage in the matching process than words that are very common in the corpus. For example let us take the matching of the following set of words:
{shipTo, billTo} and {deliverTo, invoiceTo} |
The above words when tokenized results in the following set of tokens,
{ship,To, bill, To} and {deliver, To, invoice, To} |
Here the token To is found in all the words. Hence when matching is done between the words, To is given very low weightage compared to the other words. Hence just having the token To in common doesn’t make the words similar. By combining the previously stated approaches, we were able to increase the matching efficiency considerably.
EXPERIMENTAL EVALUATION
This experiments were conducted on six datasets. Restaurant is a database of 864 restaurant names and addresses containing 112 duplicates obtained by integrating records from Fodor’s and Zagat’s guidebooks. Cora is a collection of 1295 distinct citations to 122 Computer Science research papers from the Cora Computer Science research paper search engine. The citations were segmented into multiple fields such as author, title, venue, etc. by an information extraction system, resulting in some crossover noise between the fields. Reasoning, Face, Reinforcement and Constraint are single-field datasets containing unsegmented citations to computer science papers in corresponding areas from the Citeseer scientific literature digital library. 2 Reasoning contains 514 citation records that represent 196 unique papers, Face contains 349 citations to 242 papers, Reinforcement contains 406 citations to 148 papers and Constraint contains 295 citations to 199 papers. Tables 4-6 contain sample duplicate records from the Restaurant, Cora and Reasoning datasets.
During each trial, duplicate detection was performed, at each iteration, the pair of records with the highest similarity was labeled a duplicate and the transitive closure of groups of duplicates was updated. Precision, recall and F-measure defined over pairs of duplicates were computed after each iteration, where precision is the fraction of identified duplicate pairs that are correct, recall is the fraction of actual duplicate pairs that were identified and F-measure is the harmonic mean of precision and recall Eq. 12-14:
| Table 4: | Sample duplicate records from the Cora database |
 | |
| Table 5: | Sample duplicate records from the Restaurant database |
| Table 6: | Sample duplicate records from the Reasoning database |
 | |
| Table 7: | F-measures from our experiments |
 | |
| (12) |
| (13) |
| (14) |
As more pairs with lower similarity are labeled as duplicates, recall increases, while precision begins to decrease because the number of non-duplicate pairs erroneously labeled as duplicates increases. Precision was interpolated at 20 standard recall levels following the traditional procedure in information retrieval. The result of our experimentation is shown in Table 7.
Duplicate detection is an important problem in data cleaning, record linkage and schema matching problems. We have proposed a way of combining two matching strategies along with a domain specific dictionary to increase their matching efficiency. In future we can work a way for identifying suitable learning strategies which can be used to learn matching strings in a particular domain. And also we could try other combination of matchers to see their matching efficiency in various domains.