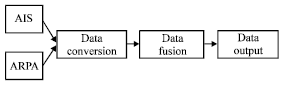
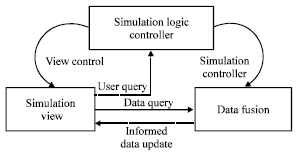
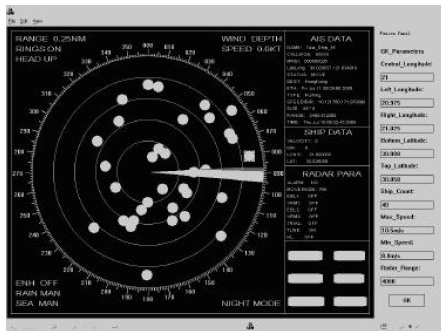
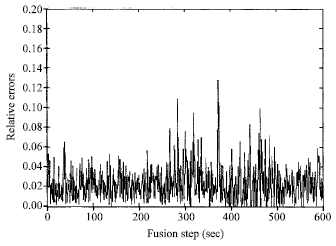
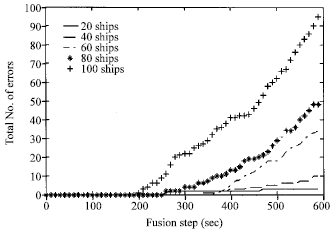
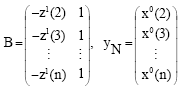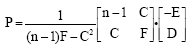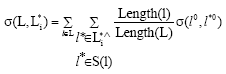Research Article
A New Model for Information Fusion based on Grey Theory
Shandong Jiaotong University Maritime College, Weihai, 264200 People�s Republic of China
Tao Wang
Shandong Jiaotong University Maritime College, Weihai, 264200 People�s Republic of China