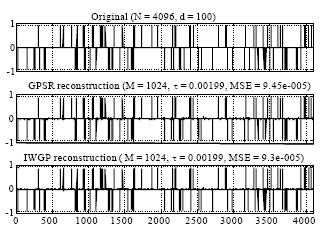
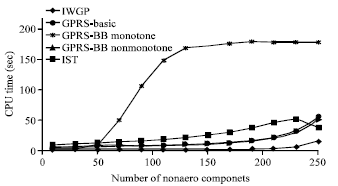
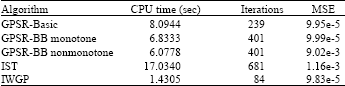
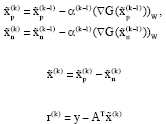Research Article
Iterative Weighted Gradient Projection for Sparse Reconstruction
School of Electronics and Information Technology, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Guanghui Ren
School of Electronics and Information Technology, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Yansheng Jin
School of Electronics and Information Technology, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Wenjing Ning
School of Electronics and Information Technology, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China