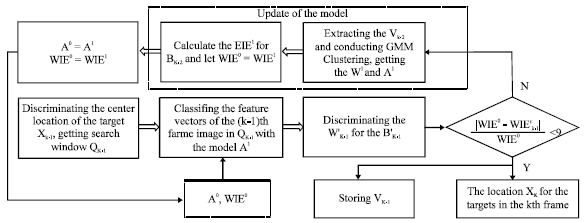
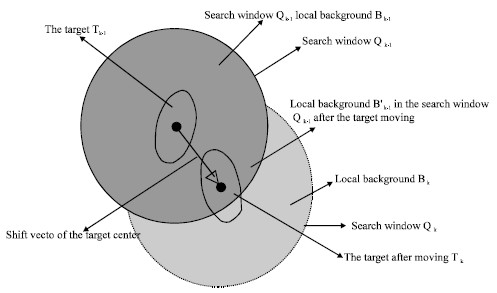
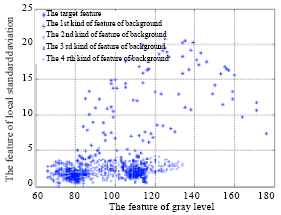
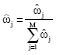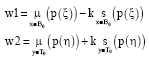Research Article
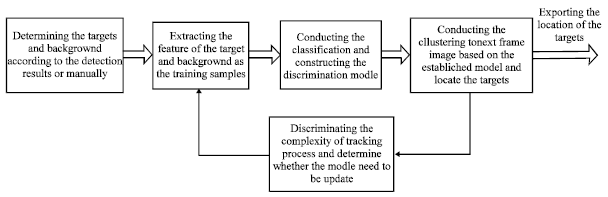
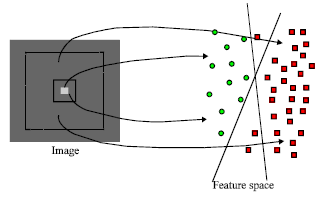
Fast Moving Small Target Tracking Based on Local Background Gaussian Mixture Model
Center for Electric Engineering and Electronics Education, Harbin University of Science and Technology, Harbin 150080, China
Sun Kai
Network Information Center, Heihe University, Heihe, 164300, China
Hou Qing-Yu
Research Center for Space Optical Engineering, Harbin Institute of Technology, Harbin 150001, China