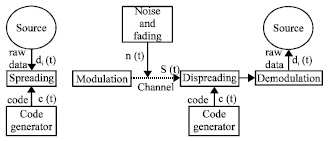
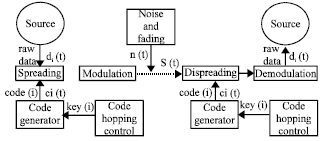
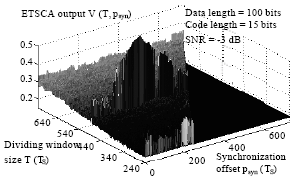
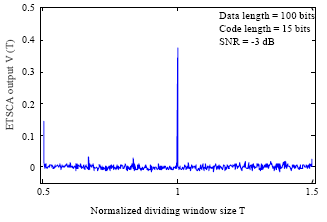
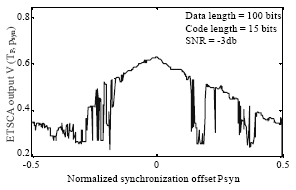
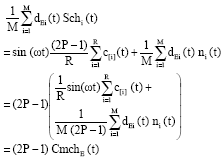
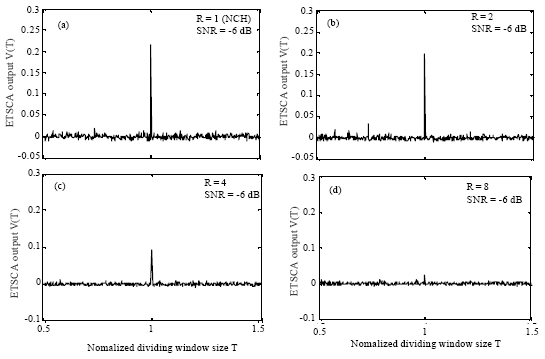
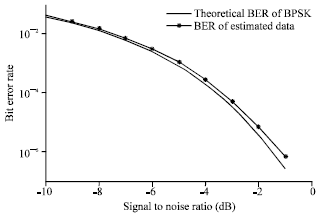
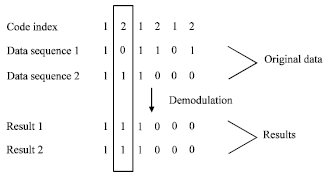
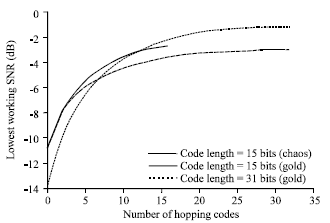
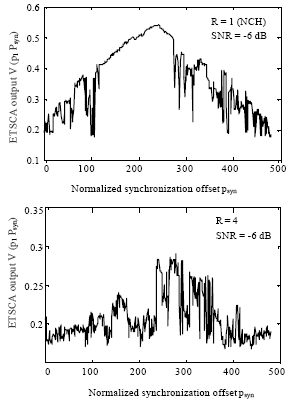
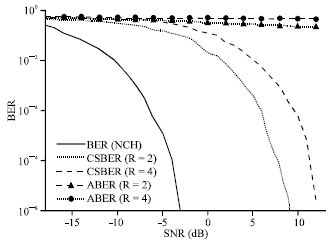
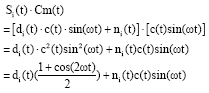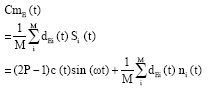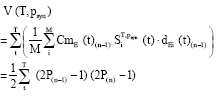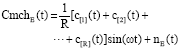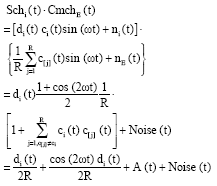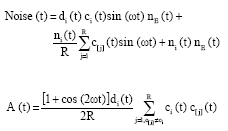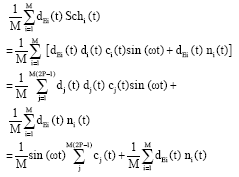Research Article
Anti-Detection Performance of Code-Hopping Direct Sequence Spread Spectrum System
Communication Research Center, Harbin Institute of Technology, Harbin, 150080, People Republic of China
Gu Xuemai
Communication Research Center, Harbin Institute of Technology, Harbin, 150080, People Republic of China
Guo Qing
Communication Research Center, Harbin Institute of Technology, Harbin, 150080, People Republic of China