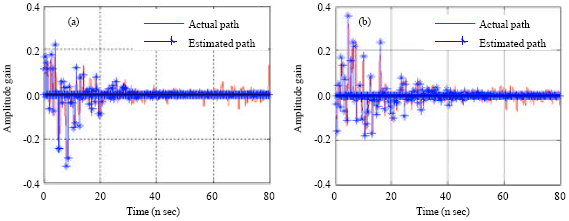
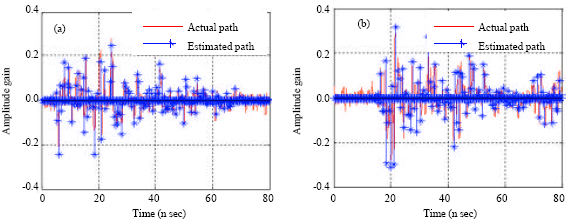
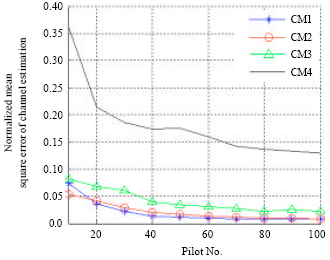
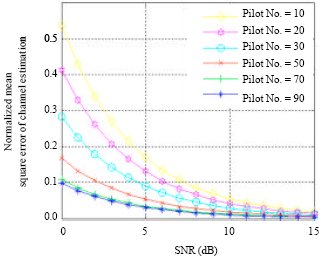
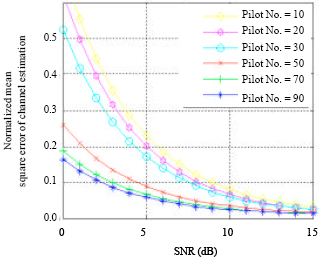
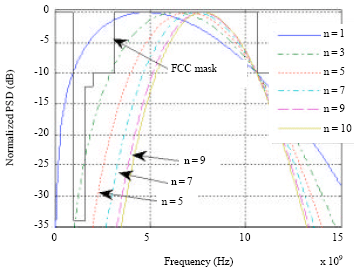
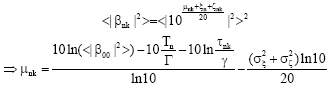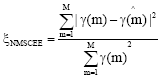Research Article
Time Domain DS-UWB Channel Estimation using Maximum Likelihood Algorithm
School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Zhenguo Shi
School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Guowei Qi
School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Yi Zhou
School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China