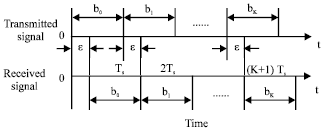
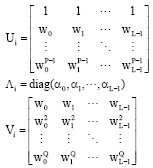
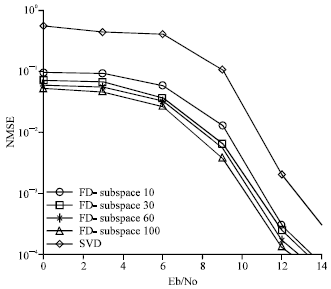
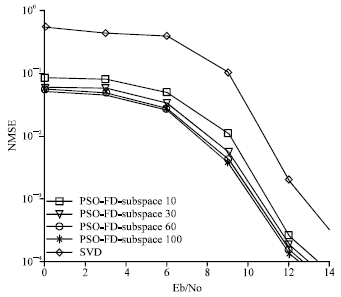
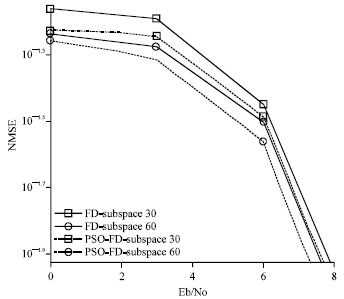
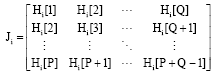Research Article
Frequency Domain Subspace Decomposition Realization of UWB Synchronization Based on PSO
College of information and Communication Engineering, Harbin Engineering University, Harbin, 150001, China
Guo Li-li
College of information and Communication Engineering, Harbin Engineering University, Harbin, 150001, China
Wan Jian
College of information and Communication Engineering, Harbin Engineering University, Harbin, 150001, China