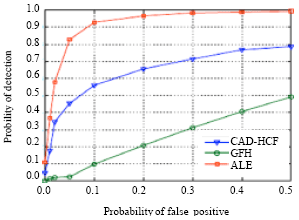
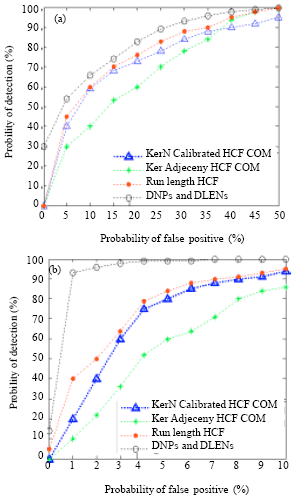
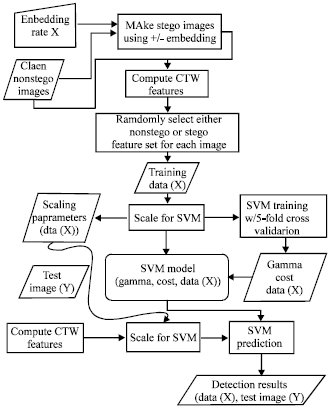
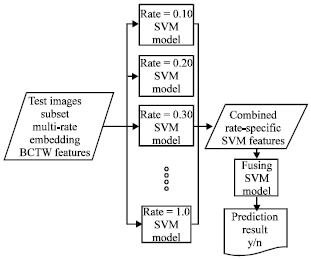
Review Article
A Review on Detection of LSB Matching Steganography
School of Computer and Information Engineering, Central South University of Forestry and Technology, Changsha, 410004, China
Xuyu Xiang
Department of Mathematics and Computer, Hunan City University, Yiyang, 413000, China
Meng Xian Wang
Department of Mathematics and Computer, Hunan City University, Yiyang, 413000, China