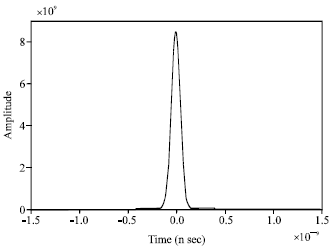
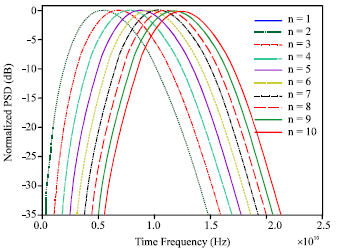
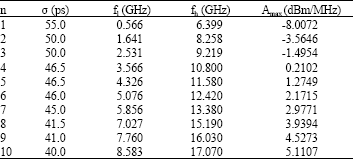
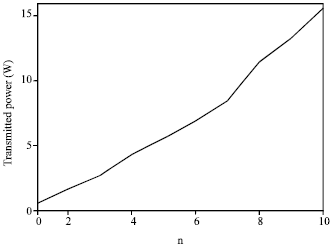
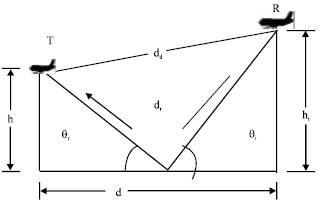
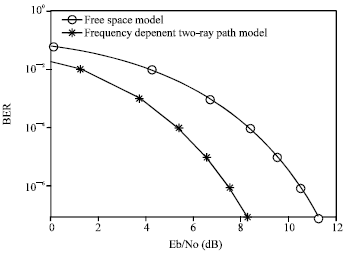
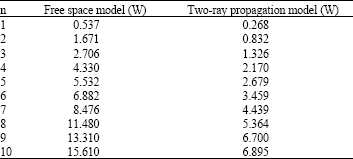
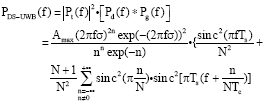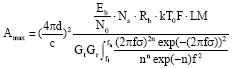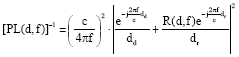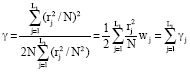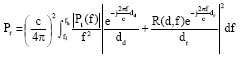Research Article
Design of Unmanned Aerial Vehicle Space Communication Links based on DS-UWB
School of Electronics and Information Engineering,Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Zhenguo Shi
School of Electronics and Information Engineering,Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Jiayang Liang
School of Electronics and Information Engineering,Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
Zhilu Wu
School of Electronics and Information Engineering,Harbin Institute of Technology, Harbin, Heilongjiang 150001, China