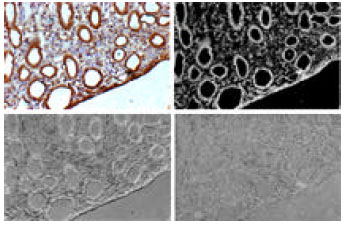
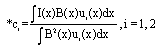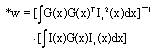Research Article
Novel Color Microscopic Image Segmentation with Simultaneous Uneven Illumination Estimation based on PCA
College of Electrical Engineering and Information Engineering,Lanzhou University of Technology, Lanzhou 730050, China
Li Zhan-Ming
College of Electrical Engineering and Information Engineering,Lanzhou University of Technology, Lanzhou 730050, China
Zhang Gui-Cang
College of Mathematics and Information Science,Northwest Normal University, Lanzhou 730070, China
Zhang Guo-Quan
College of Electrical Engineering and Information Engineering,Lanzhou University of Technology, Lanzhou 730050, China