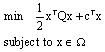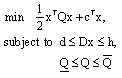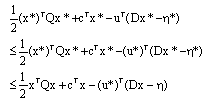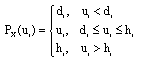Research Article
Solving Interval Quadratic Program with Box Set Constraints in Engineering by a Projection Neural Network
College of Science, Yanshan University, Qinhuangdao 066001, China
Lijun He
College of Science, Yanshan University, Qinhuangdao 066001, China
Leijie Qin
College of Science, Yanshan University, Qinhuangdao 066001, China
Tao Feng
College of Science, Yanshan University, Qinhuangdao 066001, China
Rui Shi
College of Science, Yanshan University, Qinhuangdao 066001, China