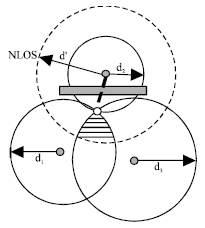
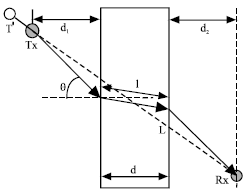
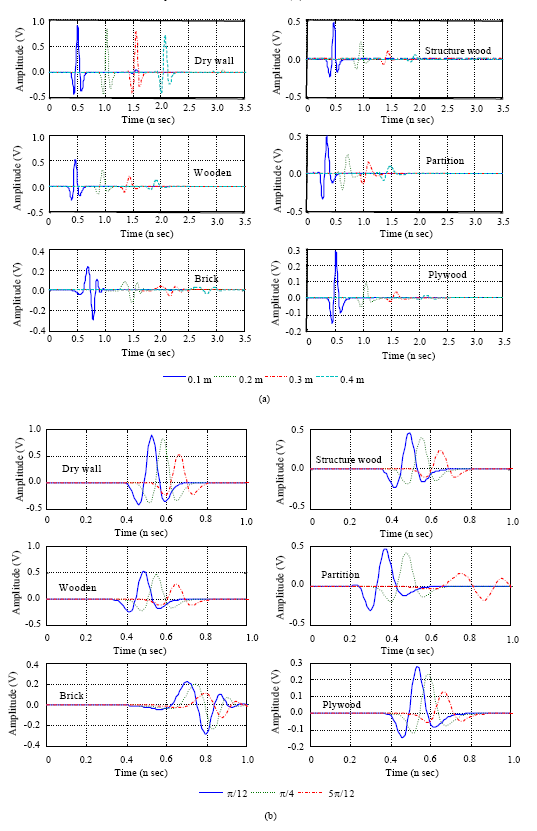
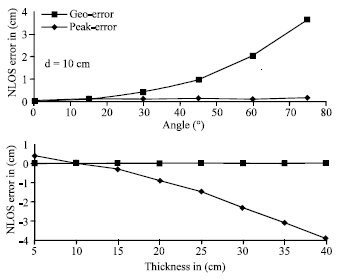
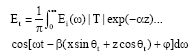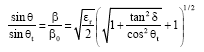Research Article
IR-UWB Waveform Distortion Analysis in NLOS Localization System
Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen, 518055, China
Zhang Nai-tong
Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen, 518055, China
Zhang Qin-yu
Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen, 518055, China