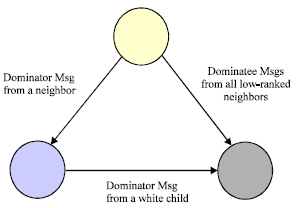
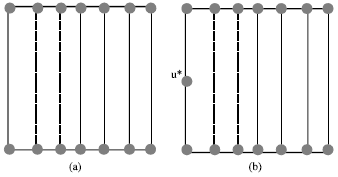
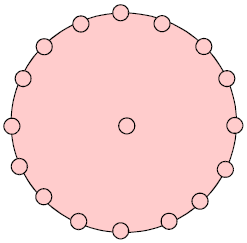
Research Article
A Survey on Connected Dominating Set Construction Algorithm for Wireless Sensor Networks
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, China
Bingwen Wang
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, China
Lejiang Guo
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, China