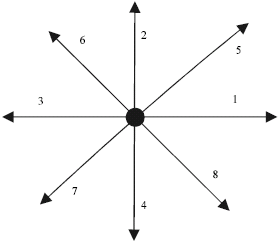
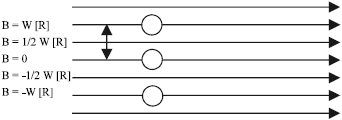
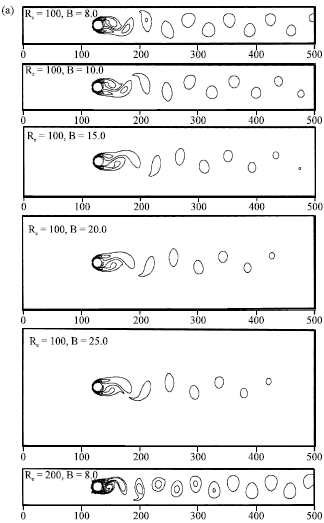
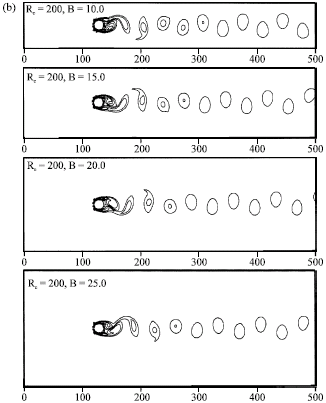
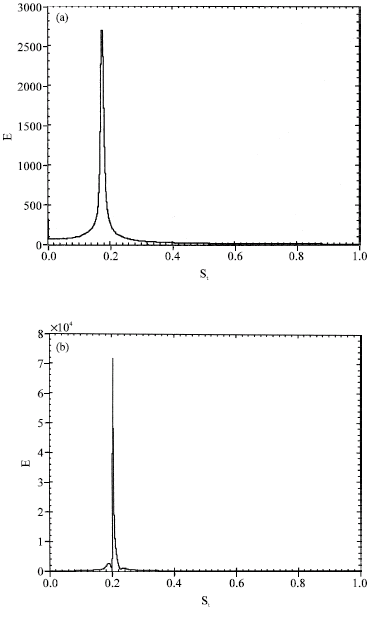
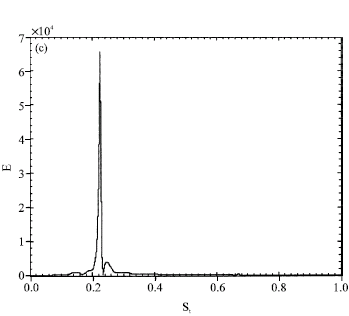
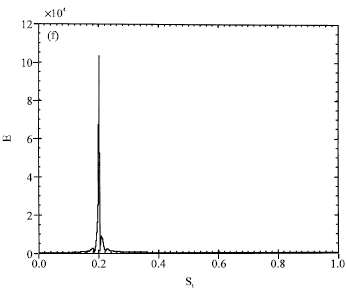
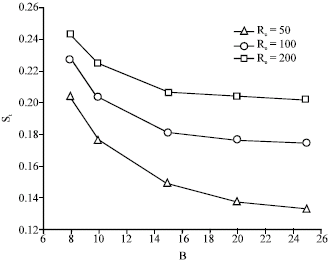
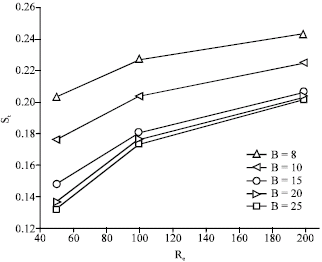
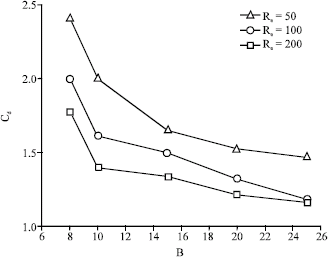
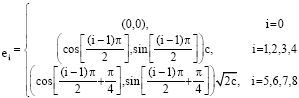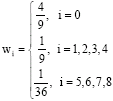Research Article
Numerical Simulation of Flow Around a Row of Circular Cylinders Using the Lattice Boltzmann Method
Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen University Town, Shenzhen 518055, China
C.Y. Zhou
Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen University Town, Shenzhen 518055, China