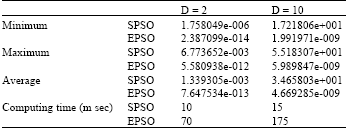
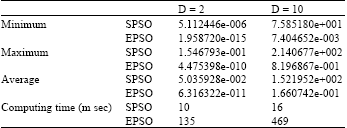
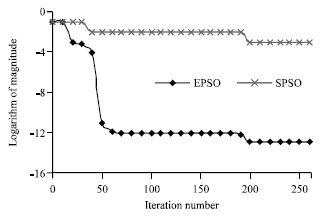
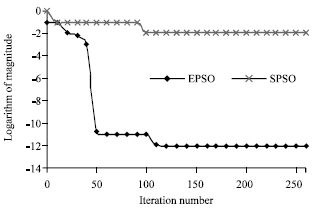
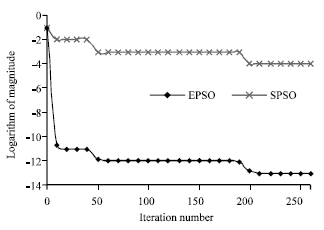
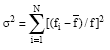Research Article
An Enhanced Particle Swarm Optimization Algorithm
School of Computer Science and Technology, Harbin University of Science and Technology, Harbin, China
Li-quan Sun
School of Computer Science and Technology, Harbin University of Science and Technology, Harbin, China
Da-song Sun
Computer Center, Harbin University of Science and Technology, Harbin, China