INTRODUCTION
Petri nets (Du et al., 2008, 2007)
are a powerful model and can model both the concurrency and parallelism in a
natural way.
For the purpose of modeling timed-driven systems, the notion of time was introduced
in Petri nets. They are known as Timed Petri Nets (TPN) (Du
et al., 2007; Vicario, 2001), which allow
all kinds of synchronization specifications.
There have been several models for describing multimedia synchronization based
on TPN.
Object Composition Petri Nets (OCPN) (Little and Ghafoor,
1990) is based on a TPN and can be used for modeling synchronization requirements
for multimedia objects. The OCPN augments Petri nets with values of time and
resources used in the places of the net. The execution of the OCPN is similar
to that of TPN where the transition firing is assumed to occur instantaneously
and the places are assumed to have states.
Extended OCPN (XOCPN) model (Woo et al., 1994)
takes into account the demands of isochronous data, requiring a rate-controlled
transmission. It is used under a network environment where several configurations
are possible for a distributed multimedia information system.
Using the OCPN and XOCPN model, it is impossible to describe modifications of the presentation sequence by a user. For instance, a user may wish to stop presentation, reverse it or skip a few frames. These operations cannot be described in the existing OCPN architecture.
Dynamic Timed Petri Nets (DTPN) (Prabhakaran and Raghavan,1993)
allows user participation to preempt the execution sequence and modify the duration
of time associated with the preempted net process. This structure can be adopted
to model multimedia synchronization characteristics with dynamic user participation.
Time Stream Petri Net (TSPN) (Senac et al., 1996)
introduces a unified formal model for the complete and accurate specification
of both temporal and logical (i.e., link) synchronization within hypermedia
distributed and weakly synchronous systems. This new model extends time Petri
nets with hierarchical design capabilities and new firing rules.
However, firing rules of DTPN and TSPN must be modified. As a result, existing analysis methods of Petri nets theory cannot be used to analyze their properties.
A logical time Petri net (Du et al., 2007) is
presented based on Petri nets. So, is a logical Petri net (Du
and Guo, 2009). Through attaching logical expressions to some actions of
a logical time Petri net model, it can model passing value indeterminacy and
describe batch processing function of cooperative systems which the existing
formal techniques cannot model.
There also exists passing value indeterminacy in multimedia synchronization when some unexpected situations occur such as data blocking, package losses and blocking timer timeout. In this case, The transitions will be fired forcibly even if data do not arrive.
In this study, logical expressions which are used to describe passing value
indeterminacy in a logical time Petri net are introduced to model multimedia
synchronization. And by referring to the previous models such as OCPN, XOCPN,
DTPN and TSPN, we present a multimedia synchronization model LTIPN which can
simply and explicitly represent basic temporal relations between multimedia
objects, multimedia synchronization and user interaction. This model provides
users simple and intuitive modeling concepts. In present model, all multimedia
synchronization events including multimedia objects are all expressed by transitions
of Petri nets, while the previous models mostly use places of Petri nets to
express multimedia objects.
LOGICAL TIME INTERACTION PETRI NET MODEL
Definition 1: A logical time interaction Petri net is a 10-tuple,
LTIPN
= (P, T, F, Dt, M, St, I, Dm, E, M) | |
where, P is a set of places; T = TM∪ TS∪ TI∪
TD is a set of transitions; TM is a set of multimedia
object transitions which denote multimedia objects, TS is a set of
logical synchronization transitions which denote multimedia synchronization,
TI is a set of user interaction transitions, TD is a set
of delay transitions; P, TM, TS, TI and TD
are disjunct sets;
F ⊆ (Px(TM∪ TS∪ TI∪ TD))∪((
TM∪ TS∪ TI∪ TD) xP)
is a set of arcs;
Dt is a function such that ∀t∈TD, Dt(t) ∈R, which
denotes the delay time of t;
M is a mapping function such that ∀t ∈ TM, M(t) is a
multimedia object and M(t) ∈ {m1,m2,...., mn};
St is a mapping function such that ∀t∈Ts, St(t) is a
logical expression fs;
I is a mapping function such that ∀t∈TI, I(t) is a user
interactive operation and I(t) ∈{skip, back, replay, pause, resume};
Dm: TM →(R+ ∪ {0})x(R+ ∪ {0})
x (R+ ∪ {0}), ∀t∈TM;Dm(t)→(x, n,
y), where the 3-tuples associated with multimedia object transitions represents
its
earliest, nominal and latest execution duration of time, respectively;
E: TM →R. ∀t∈TM, E(t)→R, where R
represents the remaining execution duration of time;
M is a marking function.
Graphically, multimedia object transitions are drawn as bars; synchronization transitions are drawn as the rectangles in which the symbol S is embedded; user interactive transitions are drawn as the rectangles in which the symbol I is embedded; delay transitions are drawn as the rectangles in which the symbol D is embedded.
|
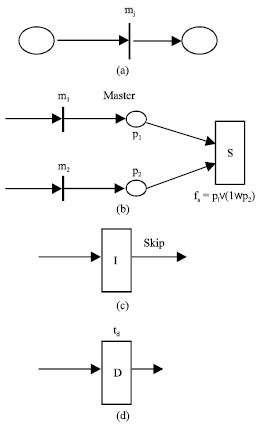| Fig. 1: |
The LTIPN representations of four classes of transitions,
(a) the representation of a multimedia object transition, (b) the representation
of a logical synchronization transition, (c) the representation of a user
interactive transition and (d) the representation of a delay transition |
For the clarity, (x, n, y) is not marked in Fig. 1a-d.
The LTIPN representations of multimedia object transitions, logical synchronization transitions, user interactive transitions and delay transitions are shown in Fig. 1.
Definition 2: Firing rules of the transitions in LTIPNs:
| • |
∀t ∈ TM, if ∀p∈Ct, M(p)
= 1, t is said to be enabled which represents the beginning of execution
of a multimedia object. t is said to be firable if E(t) = 0 which represents
the end of a multimedia object. Dm(t)→(x, n, y), in normal case, n
represents the execution duration of time of t. Firing t generates a new
marking M': ∀p∈Ct: M'(p) = M(p)-1; ∀p∈t•:
M'(p) = M(p)+1 |
| • |
∀t ∈ Ts, S(t)=fs, t is said
to be enabled if fs|M = ●T●,
i.e., all input places of t satisfy the logical input expression fI
at M; if t is enabled, it can fire and firing t generates a new marking
M': ∀p∈Ct: M'(p) = M(p)-1; ∀p∈t•: M'(p) =
M(p)+1. In some cases, the backtracking algorithm needs to be executed |
| • |
∀t ∈ TI, t is said to be enabled if
the user choose the operation I(t) and meanwhile ∀p∈Ct, M(p)
= 1; if t is enabled, it can fire and generates a new marking M': ∀p∈Ct:
M'(p)=M(p)-1; ∀p ∈ t•: M'(p) = M(p)+1. |
| • |
∀t ∈ TD, Dt(t) = td, t is
said to be enabled if ∀p∈Ct; M(p) = 1; t is said to be firable
if its enabled duration of time is equal to td and firing t results
in a new marking M': ∀p ∈ •t: M'(p) = M(p)-1; ∀p
∈ t•: M'(p) = M(p)+1 |
MODELING MULTIMEDIA REQUIREMENTS USING LTIPN
Modeling synchronization strategies: Three basic synchronization strategies
(i.e., firing rules) that favor statically or dynamically defined synchronization
units (Senac et al., 1996) are proposed:
| • |
A dynamic synchronization strategy called strong-or, driven
by the earliest processing |
| • |
A dynamic synchronization strategy called weak-and driven
by the latest processing |
| • |
A static synchronization strategy called master, driven by
a selected processing |
The three fundamental strategies entail nine firing rules obtained from a consistent
and complete combination of the absolute temporal validity interval of the synchronization
units associated with an inter-stream synchronization point (Senac
et al., 1996).
The LTIPN can simply, explicitly and directly express the three basic synchronization strategies by using logical expressions.
Master: The synchronization strategy called master, can be modeled as Fig. 2. m1 is the master multimedia object such as audio and m2 is the secondary multimedia object such as video. When transition m1 representing the master multimedia object is fired, p1 ∈ t• receives a token. The logical variable p1 = .T. The logical expression fs = p1∧(1∨p2) = .T. corresponding to the synchronization transition s. So, the synchronization transition s is fired whether p2 = .T. or not.
When the synchronization transition s is fired, it can cause two problems.
One is that some places before s still have a token after s is fired. The other
is that some transitions have not been fired before s after s is fired. These
two problems can be solved by a backtracking algorithm (Shan
et al., 2000).
Strong-or: The synchronization strategy called strong-or, can be modeled
as Fig. 3. When either p1 or p2 receives
a token, the logical expression fs = p1∨p2
= .T. corresponding to the synchronization transition s.
|
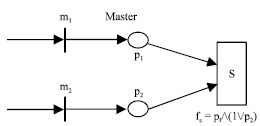| Fig. 2: |
The synchronization strategy called master |
|
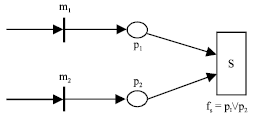| Fig. 3: |
The synchronization strategy called strong-or |
|
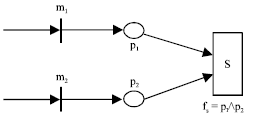| Fig. 4: |
The synchronization strategy called weak-and |
The synchronization transition s is fired. When the synchronization transition
strong-or is fired, it can also cause the above two problems and can be solved
by the backtracking algorithm like master.
Weak-and: The synchronization strategy called weak-and can be modeled as Fig. 4. When both p1 and p2 receive a token, the logical expression fs = p1∧p2 = .T. corresponding to the synchronization transition s. The synchronization transition s is fired. The other six synchronization strategies can be expressed by composing the above three basic synchronization strategies.
Modeling basic temporal relations: Given any two multimedia objects
specified by temporal intervals, there exists a LTIPN representation for their
relationship in time. LTIPN can simply, explicitly and directly describe seven
basic temporal relations between two multimedia objects. There are totally thirteen
temporal relations between two objects and the other six are inverse relations
of the six basic temporal relations. Note that the equality relation has no
inverse. The LTIPN representations of the seven basic temporal relations are
modeled as Fig. 5a-g.
|
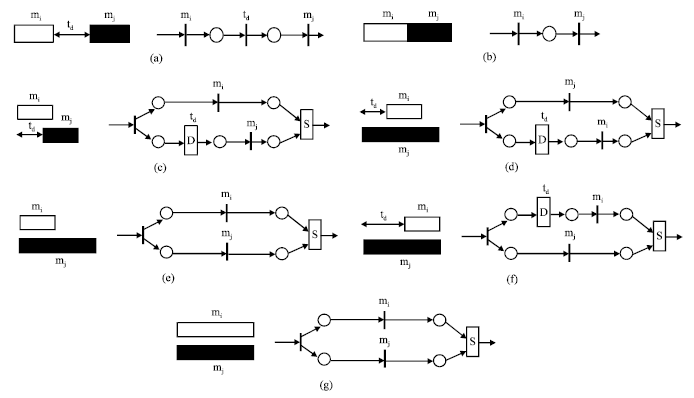| Fig. 5: |
The LTIPN representations of seven basic temporal relations,
(a) mi before mj, (b) mi meets mj,
(c) mi overlaps mj, (d) mi during mj,
(e) mi starts mj, (f) mi finishes mj
and (g) mi equals mj |
|
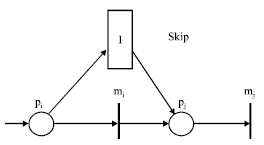| Fig. 6: |
The LTIPN representation of the skip operation |
Modeling user interaction: A user should be allowed to manipulate the
presentation sequence in multimedia systems either through a program or by key-board/mouse
input (Prabhakaran and Raghavan, 1993). The LTIPN can
describe some multimedia synchronization with user participation such as skip,
back, replay, pause and resume.
Skip: The skip operation can be modeled as Fig. 6. When a user chooses the skip operation and pi ∈Ct has a token at the same time, the user interactive transition skip is fired. pi removes a token and the remaining duration of time e associated with mi is reset and pj ∈ t• receives a token, the transition representing a multimedia object mj is enabled and mj is started.
Back: The back operation can be modeled as Fig. 7.
When a user chooses the back operation and pj ∈Ct has a token
at the same time, the user interactive transition back is fired. pj removes
a token and the remaining duration of time e associated with mj is
reset. pi ∈ t• receives a token, the transition representing
a multimedia object mi is enabled and mi is started.
|
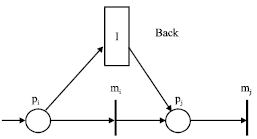| Fig. 7: |
The LTIPN representation of the back operation |
|
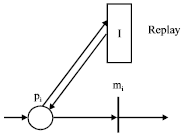| Fig. 8: |
The LTIPN representation of the replay operation |
Replay: The replay operation can be modeled as Fig. 8.
When a user chooses the replay operation and pi ∈Ct has a token
at the same time, the user interactive transition replay is fired. pi removes
a token and the remaining duration of time e associated with mi is
reset.
|
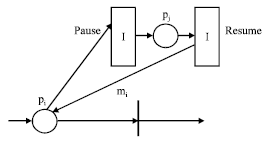| Fig. 9: |
The LTIPN representation of the pause and resume operation |
Then pi ∈ t• receives a token again, the transition
representing a multimedia object mi is enabled and mi is
restarted.
Pause and resume: The pause and resume operation can be modeled as Fig. 9. When a user chooses the pause operation and pi ∈Ct has a token at the same time, the user interactive transition pause is fired. pi removes a token and the remaining duration of time e associated with mi is saved. Then, pj ∈ t• receives a token.
When a user chooses the resume operation and pj ∈Ct has a token at the same time, the user interactive transition resume is fired. pi ∈ t• receives a token again. The transition representing a multimedia object mi is enabled again. However, because the remaining duration of time e associated with mi is not the initial value and mi only show the remaining duration of time e.
CONCLUSIONS
A multimedia synchronization model LITPN for describing multimedia synchronization is designed in this study. In this model, we classify transitions into four categories: multimedia object transitions, multimedia synchronization transitions with logical expressions, user interaction transitions and delay transitions. These transitions express multimedia synchronization in a natural and intuitive way.
Further study is to develop an algorithm for building the LTIPN reachability graph to perform some analysis, thus allowing to check the real time properties and the consistency of multimedia systems. Also, we intend to develop a tool for the modeling and analysis of LTIPN models.
ACKNOWLEDGMENTS
This study is supported in part by the National Natural Science Foundation of China under Grants 60773034, 90818023, 90718012 and 60803032; the Taishan Scholar Construction Project of Shandong Province, China; the Scientific and Technological Developing Program of Shandong Province of China under Grant 2008GG30001024 and the Open Project of the State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences under Grant SYSKF0804; the Research Project of SUST Spring Bud in Shandong University of Science and Technology in 2009 and the Graduate Innovation Fund of Shandong University of Science and Technology.
Subscribe Today
