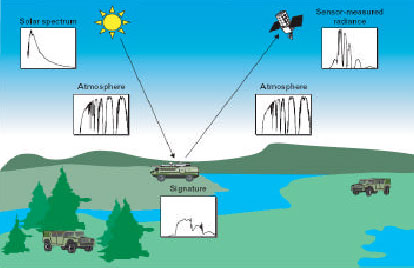
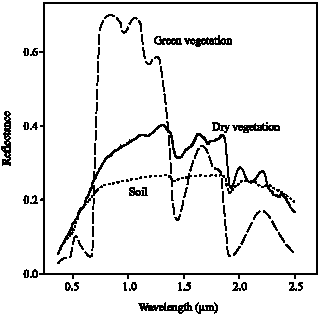
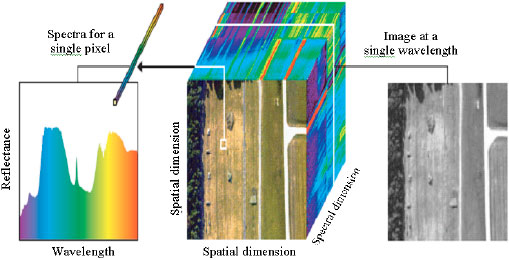
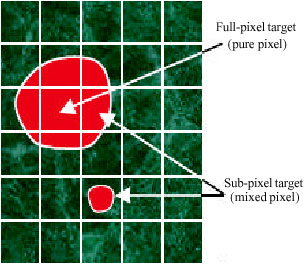
Research Article
Super-Resolution Challenges in Hyperspectral Imagery
Institute of Image and Information Technology,Harbin Institute of Technology, 150001, People`s Republic of China
Ye Zhang
nstitute of Image and Information Technology,Harbin Institute of Technology, 150001, People`s Republic of China
Humayun Karim Sulehria
Institute of Image and Information Technology,Harbin Institute of Technology, 150001, People`s Republic of China
Asad Babakhani
NRPD, Iran National Regulatory Authority, Iran
Mohammad Reza Kardan
NRPD, Iran National Regulatory Authority, Iran