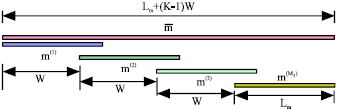
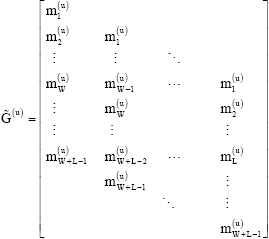
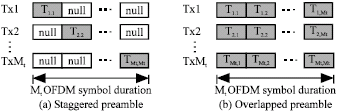
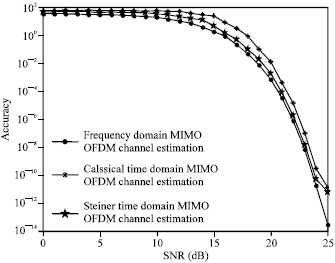
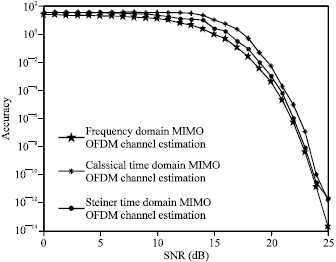
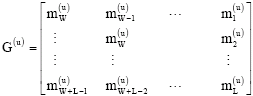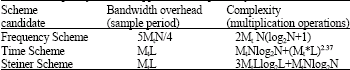Research Article
A New Steiner Channel Estimation Method in MIMO OFDM Systems
Department of Information and Communication Engineering, Xi`an Jiaotong University, Peoples`s Republic of China
Wang Liejun
Department of Information and Communication Engineering, Xi`an Jiaotong University, Peoples`s Republic of China
Zhang Taiyi
Department of Information and Communication Engineering, Xi`an Jiaotong University, Peoples`s Republic of China
Runping Yun
Department of Information and Communication Engineering, Xi`an Jiaotong University, Peoples`s Republic of China