ABSTRACT
In this study, we focus on the impact of combining the decision support system and the continuous review integrated inventory model involving controllable lead time, ordering cost and backorders. The objective is to establish a decision support system with integrated inventory model to minimize the joint total expected inventory cost by simultaneously considering ordering cost, ordering quantity, safety factor, lead time, backorder discount and the number of lots delivered from vendor to buyer. Because the reduction of inventory cost plays an important role in production management, this research builds a decision support system to deal with the integrated inventory model. In the decision support system concerning about the inventory model, we take both the vendor and the buyer into account and help the decision maker to make decisions.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/itj.2007.1069.1074
URL: https://scialert.net/abstract/?doi=itj.2007.1069.1074
INTRODUCTION
Some time ago, the companies can be obtained the competitive advantage by strengthening their competitiveness. Therefore we can use the integrated inventory model to obtain minimum the total relevant cost for both vendor and buyer. The JIT’s approach to productivity demands that small lots be run in production. This can only be achieved if the setup time is reduced. The ability to reduce setup costs over time can be explained in terms of the learning curve.
Lead time has played an important role in inventory management in recently. Although lead time can be constant or variable, it is often treated as a prescribed parameter in most of the inventory management literature. Therefore, the lead time crashing cost function is a piecewise linear function (Liao and Shyu, 1991; Ouyang and Chang, 2002; Ouyang et al., 1999).
In traditional economic order quantity EOQ models, ordering cost is treated as a constant. Applying the EDI technology is not only linking but also automate the ordering, shipping, inquiring and payment activities between vendor and buyer (Porteus, 1985; Porteus, 1986; Trevino et al., 1993; Woo et al., 2001).
In today’s supply chain management environment, companies are using the JIT production to obtain maintain a competitive advantage and requires a spirit of cooperation between the buyer and the vendor. Many researchers have shown that buyer and vendor can obtain greater benefit through strategic cooperation with each other (Goyal, 1988; Banerjee, 1986; Ha and Kim, 1997; Pan and Yang, 2002; Huang, 2002).
The shortage cost is one of the four types of cost relevant to inventory management decisions. Pan et al. (2004) extended Pan and Hsiao’s (2001) model by considering the reorder point as a decision variable and the crashing cost per unit time is in proportion to the reduced lead time and the order quantity. They also apply the minimax distribution free approach to solve the inventory model.
Cheng (1991) argued that the reduction in lot size and savings in total inventory cost based on Replogle’s (1988) model seem to be over estimated due to the way in which Replogle defines the learning curve, which is different from traditional definition.
In this study, we consider this model in which ordering quantity, ordering cost, safety factor, lead time and backorder discounts are decision variables. Furthermore, an algorithm is applied to find the optimal solution for the case where the lead time demand follows a general distribution. Numerical example is included to illustrate the integrated algorithm procedures. Next we construct a decision support system to analysis the integrated model, then find out the best choice between the vendor and the buyer. Once we build the decision support system, we can use the result to apply into other inventory model and adjust the parameter to fit the other different inventory situations.
ASSUMPTIONS
| • | There is single vendor and single buyer for a single production in this model. |
| • | Inventory is continuously reviewed. The buyer places an order or requests successive shipment when the on hand inventory reaches the reorder point. |
| • | The product is manufactured with a finite production rate P and P>D. |
| • | Lead time L is deterministic and lead time demand X has finite mean DL and standard deviation |
| • | The reorder point r = expected demand during lead time + safety stock (SS), that is r = DL+k |
| • | The lead time L has n mutually independent components and these are crashed one component at a time starting with the one with the least crashing cost per unit time and so on. |
| • | We assume that the capital investment, I(A), in reducing ordering cost is a logarithmic function of the ordering cost A. That is, |
| • | The backorder ratio β is variable and is in proportion to the backorder price discount offered by the buyer per unit π x; thus, β = β 0π x/π 0 for 0<β 0≤ 1 for 0≤π x≤π 0. |
| • | The extra costs incurred by the vendor will be fully transferred to the purchaser if shortened lead time is requested. |
THE INTEGRATED INVENTORY MODEL
In this section, we illustrate how to establish an integrated inventory model. In our model, shortages consist of a mixture of backorders and lost sales are allowed. In order to increase service level, we supply a backorder price discount. Besides, lead time is controllable and can be reduced by additional crashing cost (Fig. 1). Eventually, we consider the reducing ordering cost and the learning effect on setup.
The joint total expected cost can be expressed as:
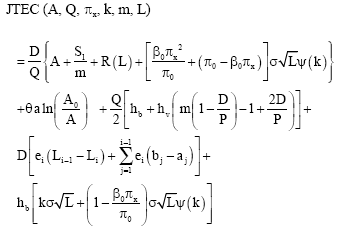 |
where:
Due to the probability distribution of the lead time demand X is unknown. Hence, we use the minimax distribution free approach to find the (A, Q, π x, k, m, L) with the optimal expected total inventory cost. This method is to find the minimum value among the highest possible expected total inventory cost over all the decision variables. Gallego and Moon (1993) proved that for any F∈Ω
Because ![]() . Therefore, the objective function is reduced to minimize
. Therefore, the objective function is reduced to minimize
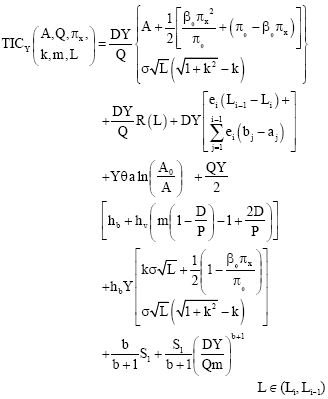 |
DECISION SUPPORT SYSTEM
Sprague and Carson (1982) thought a complete framework of decision support system should include the following events shown as Fig. 2:
| • | Data Base: Store up the data that the decision support system requires. |
| • | Model Base: Store up the data analysis model and decision analysis model or view these models as sub-patterns which are independent with each other. |
| • | Software System: The software system includes the following three subsystems (Fig. 2-4). |
| • | Data Base Management Subsystem, DBMSs. |
| • | Model Base Management Subsystem, MBMSs. |
| • | Dialog Generation and Management Subsystem, DGMSs. |
 | |
| Fig. 1: | The illustration of the integrated algorithm |
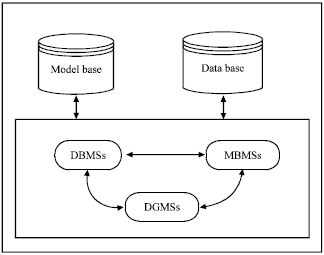 | |
Fig. 2: | DSS system framework |
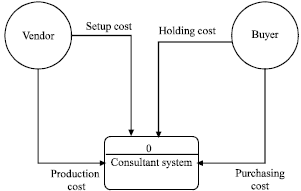 | |
Fig. 3: | Panorama diagram |
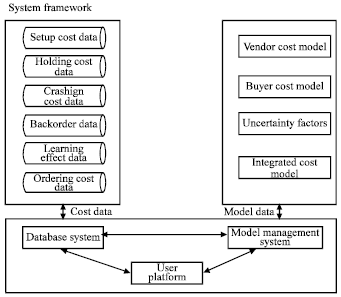 | |
Fig. 4: | System framework |
The procedure of the integrated operation model is shown as in Fig. 5.
| • | Step 1:Combine the vendor and the buyer cost models. |
| • | Step 2:Consider the cost factors. |
| • | Step 3:Integrated operation. |
| • | Step 4:Total analysis. |
| • | Step 5:Output. |
Numerical example: In order to illustrate the above solution procedure, we consider an inventory problem has the following data: D = 800 units per year, P = 3,000 units per year, S1 = $300 per set-up, A0 = $150 per order, hv = $15 per unit per year, hb = $20 per unit per year, σ = 7 units per week, π 0 = $150 per unit, Y = 1 year of period and the lead time data is shown in Table 1.
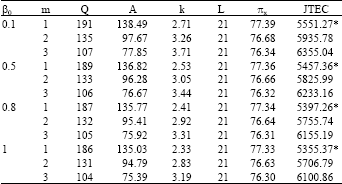
In addition, for ordering reduction, we take θ = 0.1 per dollar per year and a = 5800. We suppose the demand during lead time is unknown, then applying the above integrated algorithm to solve the inventory problem for β 0 = 0.1, 0.5, 0.8 and 1. The result of solution procedure is showed in Table 2.
The number marked with * is the optimal solution for a given β 0. Table 2 shows the optimal solutions with β 0 = 0.1, 0.5, 0.8, 1, respectively.
| Table 1: | Lead time data of the numerical example |
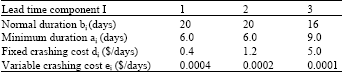 | |
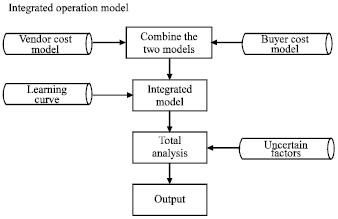 | |
| Fig. 5: | Integrated operation model |
| Table 2: | Results of numerical example (L in days, Y = 1) |
 | |
CONCLUSIONS
In this study, When the distribution of lead time demand is unknown and the cumulative distribution functions with finite mean μ L and variance σ 2L, we utilize the minimax distribution free procedure to deal with the distribution free model. The purpose of our study is to establish an integrated inventory model to minimize the joint to total expected inventory cost. We develop a DSS procedure to find the optimal solution and help the manager to take decisions.
This study presents a continuous review integrated inventory model and assumed the item is perfect. From the production management point of view, the efficiency of inventory decision support system will affect the inventory decision achievements. Hence, we shall pay resources to establish the suitable inventory decision support system. Further, if the inventory situation changes, the manager still can do the best decision in a short time. In future research on this problem, it can consider the periodic review integrated inventory model, or change the assumption that the item is perfect to consider defective item.
ACKNOWLEDGMENTS
The author would like to thank the referees for their helpful comments and suggestions and the financial support of National Science Council of Taiwan (NSC 95-2221-E-231-018).
NOTATION
The notation used in the paper is as follows:
| Q | = | The order quantity of the buyer (decision variable); |
| A | = | Buyer’s ordering cost per order (decision variable); |
| k | = | Safety factor (decision variable); |
| m | = | A positive integer representing the number of lots in which the items are delivered form the vendor to the buyer in one production cycle (decision variable); |
| L | = | Length of lead time (decision variable); |
| π x | = | Backorder price discount offered by the buyer to the customer (decision variable); |
| D | = | Average demand rate per year on the buyer; |
| p | = | Vendor’s production rate; |
| S1 | = | Vendor’s first set-up cost; |
| hv | = | Vendor’s holding cost per item; |
| hb | = | Buyer’s holding cost per item; |
| π 0 | = | Marginal profit per unit; |
| β | = | The backorder ratio, 0≤β≤ 1; |
| β 0 | = | The upper bound of the backorder ratio; |
| A0 | = | Original ordering cost; |
| I(A) | = | Capital investment required to achieve ordering cost A, 0<A≤ A0; |
| θ | = | Fractional opportunity cost of capital; |
| δ | = | Percentage decrease in ordering cost A per dollar increase in investment I(A); |
| X | = | The lead time demand which has a distribution function (d.f) F with finite mean DL and standard deviation |
| Φ | = | The standard normal cumulative distribution function; |
| φ | = | The standard normal distribution; |
| B(r) | = | The expected stock-out of a cycle; |
| Y | = | Number of years; |
| b | = | The logarithm of learning rate divided by the log of 2. |
REFERENCES
- Banerjee, A., 1986. A joint economic lot size model for purchaser and vendor. Dec. Sci., 17: 292-311.
CrossRef - Gallego, G. and I. Moon, 1993. The distribution free newsboy problem: Review and extensions. J. Operat. Res. Soc., 44: 825-834.
Direct Link - Ha, D. and S.L. Kim, 1997. Implementation of JIT purchasing: An integrated approach. Prod. Plan. Control, 8: 152-157.
CrossRef - Huang, C.K., 2002. An integrated vendor-buyer cooperative inventory model for items with imperfect quality. Prod. Plann. Control, 13: 355-361.
Direct Link - Liao, C.J. and C.H. Shyu, 1991. An Analytical determination of lead time with normal demand. Int. J. Operat. Prod. Manage., 11: 72-78.
Direct Link - Ouyang, L.Y., C.K. Chen and H.C. Chang, 1999. Lead time and ordering cost reductions in continuous review inventory systems with partial backorders. J. Operat. Res. Soc., 50: 1272-1279.
Direct Link - Ouyang, L.Y. and H.C. Chang, 2002. Lot size reorder point inventory model with controllable lead time and set-up cost. Int. J. Syst. Sci., 33: 635-642.
Direct Link - Pan, J.C.H. and Y.C. Hsiao, 2001. Inventory models with back-order discounts and variable lead time. Int. J. Syst. Sci., 32: 925-929.
Direct Link - Pan, J.C.H. and J.S. Yang, 2002. A study of an integrated inventory with controllable lead time. Int. J. Prod. Res., 40: 1263-1273.
Direct Link - Pan, J.C.H., M.C. Lo and Y.C. Hsiao, 2004. Optimal reorder point inventory models with variable lead time and backorder discount considerations. Eur. J. Operat. Res., 158: 488-505.
CrossRef - Porteus, E.L., 1986. Optimal lot sizing, process quality improvement and setup cost reduction. J. Operat. Res. Soc., 34: 137-144.
Direct Link - Trevino, J., B.J. Hurley and W. Friedrich, 1993. A mathematical model for the economic justification of setup time reduction. Int. J. Prod. Res., 31: 191-202.
Direct Link - Woo, Y.Y., S.L Hsu and S. Wu, 2001. An integrated inventory model for a single vendor and multiple buyers with ordering cost reduction. Int. J. Prod. Econ., 73: 203-215.
CrossRef








