Research Article
Deblocking in BDCT Image and Video Coding Using a Simple and Effective Method
Department of Electronic and Communication Engineering, Faculty of Mechanical and Electrical Engineering, Damascus University, Syria
The block-based Discrete Cosine Transform (BDCT) is used in most image and video coding standards including JPEG, MPEG and the ITU family of video compression standards (H.261, H.263) (Lai et al., 1995; 1996). The performance of BDCT techniques approaches that of the optimal Karhumen-Loeve transform (Lai et al., 1995; 1996). However, in cases of high compression ratios such as low-bit-rate applications, BDCT results in unpleasant blocking artifacts or blocking effect that manifests itself as artificial horizontal and vertical boundaries between the blocks. The blocking effect is due to independent quantization in neighboring blocks of BDCT coded image (Lai et al., 1996). The characteristics of the Human Visual System (HVS) contribute to a worsened perception of blocking artifacts (Castagno et al., 1998). HVS is naturally sensitive to edges, especially vertical and horizontal boundaries in uniform or smooth regions. The problem of the blocking effect is complicated by its nonlinear nature and the complicated behavior of the HVS, which is also nonlinear (Castagno et al., 1998).
Many researches have been carried out for reducing the blocking artifacts without significant degradation of other characteristic of the compressed image quality (Reeves and Lim, 1984; Wang et al., 2000). We propose a simple and effective deblocking method using an adaptive filtering. The effectiveness of the proposed method is evaluated subjectively and objectively. As an objective measure of the reconstructed image quality we use PSNR (peak signal-to-noise ratio) (Cho, 2001; Rowe, 1997). The PSNR measure is used in most image and video compression applications, because it is the most common and the easiest to compute (Cho, 2001; Rowe, 1997).
PROPOSED DEBLOCKING METHOD
Based on the following observations, we propose an adaptive deblocking method using spatial low-pass filtering. The proposed method performs one-dimensional filtering along the boundaries of an 8x8 blocks as well as the block borders. The filtering process consists of a suitable classification into three modes and applying filtering according to the proposed classification.
Observations related to deblocking: We propose an adaptive spatial low-pass filtering for deblocking. The low-pass filtering approach proved very successful in reducing the blocking effect (Reeves and Lim, 1984), but it may degrade the sharpness of image details and edges (Lee et al., 1998; Ramkishor and Karandikar, 2000). Hence, trying to reduce the blocking artifacts we consider the following observations (Kim et al., 1999).
| • | HVS is more sensitive to the blocking effect in smooth areas than in detailed areas. |
| • | When we apply filtering locally for pixels directly adjacent to block boundaries, altering the values of these pixels can lead to new discontinuity between each altered boundary pixel and the pixel immediately adjacent to it within the block (Chou et al., 1998). |
| • | In video coding, the blocking artifacts of the previous frame can be propagated to the current frame due to motion compensated prediction (Kim et al., 1999). |
According to the first observation we apply strong filtering along the block boundaries in smooth areas and weak filtering in detailed areas.
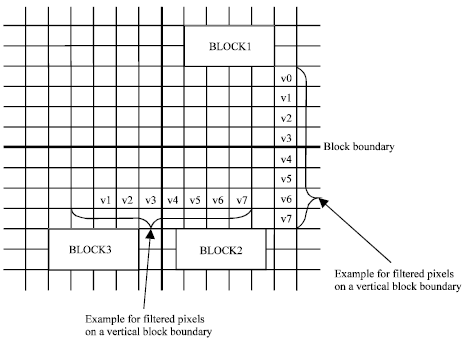 | |
| Fig. 1: | Examples of positions of pixels |
Considering the second and third observations, we apply filtering in smooth areas inside the blocks as well as on the block boundaries (Kim et al., 1999; Chou et al., 1998).
Classification: In the proposed deblocking method we adapt filtering to the local characteristics of the image considering the observations above. We classify the image areas by computing the following function, employed by Shen et al. (1999) and Abboud (2005), according to pixel positions in Fig. 1.
| (1) |
where Φ(Δ)=1 if |Δ| is less than a threshold T1 and Φ(Δ) is set to zero, otherwise. The value of T1 is selected 3 as by Shen et al. (1999). The function count reflected the “flatness” of the local image area across a block boundary (Kim et al., 1999; Shen et al., 1999). We will employ the following classification.
| • | The image area across a block boundary is considered flat or very smooth if the value of count equals 6. |
| • | The related image area is considered relatively smooth if the value of count equals by 1, 2, 3, 4 or 5. |
| • | The image area is considered highly detailed or complex, if the count equals 0. |
This classification is a modified version of the classification applied by Kim et al. (1999) and Shen et al. (1999).
Proposed filtering approach: We propose a relatively simple adaptive filtering approach, taking into consideration the earlier mentioned observations.
Instead of relatively complicated filtering approached by Ramkishor and Karandikar (2000) and List et al. (2003), we use the following function, applied by Abboud (2005) and used by Burt and Adelson (1983) for other applications.
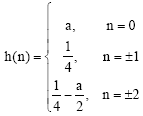 | (2) |
We employ the function h(n) for filtering, as an “impulse response”. The corresponding equivalent weighting functions, according to (Burt and Adelson, 1983) are shown in Fig. 2 for three values of a. The equivalent weighting function in Fig. 2 is triangular for a = 0.5, whereas it is Gaussian-like for a = 0.4 and when a = 0.3 the curve is flatter and broader than a Gaussian. We select a = 0.3 for relatively strong filtering, a = 0.4 for moderate filtering and a = 0.5 for weak filtering.
We apply the function h(n) horizontally to filter the vertical block boundaries, replacing a pixel value v(x, y) by the value:
| (3) |
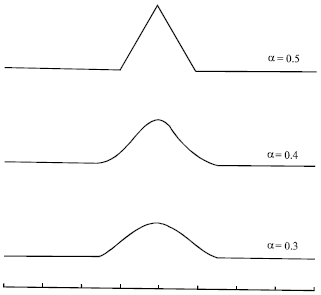 | |
| Fig. 2: | The equivalent weighting functions, employed for filtering |
We apply h(n), also, vertically to filter the horizontal block boundaries, replacing v(x, y) by the value:
| (4) |
Two proposed algorithms: We propose two algorithms for deblocking using three-mode adaptive filtering.
Algorithm 1: We apply the proposed classification and the proposed adaptive filtering according to the following algorithm.
Along every vertical block boundary
| • | Compute count according to (1) and Fig. 1. |
| • | If count equals 6 (i.e., if the region is flat), then apply (3) and (2) to: compute v3 and v4, using h(n) for a = 0.3, compute v2 and v5, using h(n) for a = 0.4, compute v1 and v6, using h(n) for a = 0.5. |
| • | If count equals 1, 2, 3, 4 or 5 (i.e., if the region is relatively smooth), then apply (3) and (2) to: compute v3 and v4, using h(n) for a = 0,4, compute v2 and v5, using h(n) for a = 0.5. |
| • | If count equals 0 (i.e. if the region is complex), then apply (3) and (2) to: compute v3 and v4, using h(n) for a = 0.5. |
The previous steps are applied horizontally along all vertical boundaries first and then vertically along all horizontal boundaries using (4) instead of (3).
 | |
| Fig. 3: | The original Lena test image |
If a pixel value is changed by the first filtering operation (horizontally), the updated pixel value is used for next filtering (vertically). This approach is applied by Abboud (2005) and partly similar to the approach by Chou et al. (1998).
Algorithm 2: In this algorithm we perform all steps of algorithm 1, except for pixels which are filtered in both directions (horizontally and vertically). For these pixels the two filtering operations are performed independently and then we average the two resulting values (Such averaging approach is applied in by Wang et al. (1998) for block corners).
RESULTS OF APPLYING THE TWO ALGORITHMS
We applied software programs realizing the two algorithms to a Lena test image (a Bitmap image, having 512x512 pixels), shown in Fig. 3. The BDCT method was applied and then the image was reconstructed using small numbers of the DCT coefficients (first without applying our deblocking algorithms and then after applying them). We executed the programs several times, using different numbers of DCT coefficients for the reconstruction of the image. We consider that reducing the numbers of used DCT coefficients is nearly equivalent to increasing the quantization step (e.g., when using JPEG for high compression ratios) from the viewpoint of increasing the compression ratio and, also, from the viewpoint of the visual appearance of the blocking effect. Figure 4 and 5 show the central part of the Lena image before and after applying Algorithm 1, when using 2x2 and 3x3 DCT coefficients.
 | |
| Fig. 4: | The central part of Lena image, when using 2x2 DCT coefficients: a) before deblocking, b) after applying Algorithm 1 |
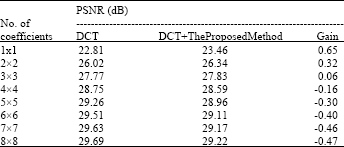
It is clear from Fig. 4 and 5 that Algorithm 1 effectively reduces the blocking effect with slight degradation of the sharpness of image details. We found that after applying Algorithm 2 the resulting images are visually nearly similar to those obtained after applying Algorithm 1 for the same numbers of DCT coefficients. For the objective evaluation of the overall reconstructed image quality after applying the two algorithms, we computed the PSNR values for different numbers of the used DCT coefficients. The resulting PSNR values are presented in Table 1 and 2 for the same Lena image. The PSNR gain in Table 1 and 2 represents the PSNR improvement.
 | |
| Fig. 5: | The central part of Lena image, when using 3x3 DCT coefficients: a) before deblocking, b) after applying Algorithm 1 |
It may be compared in some applications with a threshold of 0.5 dB, used by the MPEG committee as an informal threshold indicating minimum significant change of the overall image quality. However, if a deblocking algorithm effectively reduces the blocking artifacts a small PSNR improvement such as 0.1 dB may be considered important (Ramkishor and Karandikar, 2000).
| Table 1: | PSNR results for Algorithm 1 |
 | |
| Table 2: | PSNR results for Algorithm 2 |
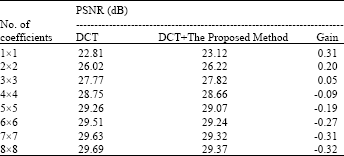 | |
Comparing Table 1 and 2 we see an improved performance of Algorithm 1 over Algorithm 2 for cases of small numbers of used DCT coefficient. This may be explained by the side effects resulting after applying Algorithm 2 due to averaging, which doesn’t suit the nonlinear nature of blocking effect.
In general, the obtained results show that the two algorithms effectively reduce blocking artifacts with slight enhancement or degradation of overall image quality. The effectiveness of the two proposed algorithms may be considered good, taking into account their relative simplicity, e.g., comparing with the filtering algorithm employed by Kim et al. (1999) and Shen et al. (1999). The relative simplicity is very important for real-time applications of video coding (Shen et al., 1999).
CONCLUSIONS
In this study we proposed a simple and effective method for deblocking in BDCT-based image and video coding. To reduce the blocking effect without significant degradation of the sharpness of image edges and details, the proposed method uses a three-mode adaptive filtering. We presented two relatively simple algorithms according to the proposed method. We applied the two algorithms for the Lena test image. The obtained results show relatively good effectiveness of both algorithms, despite their relative simplicity. The simplicity of the proposed algorithms is very important for real-time applications of video coding.