Research Article
Elliptic Curve Cryptography over Binary Finite Field GF(2m)
Department of Physics, Eastern Mediterranean University, Gazirnagusa, North Cyprus, via Mersin 10, Turkey
In the modern information-oriented society, various devices are connected to the Internet as terminals, which necessitate technology for information security. Today, the world continues to witness an explosion of technology designed to help people communicate faster and more easily. We carry powerful digital computers in our pockets, exchange digital information in addition to voice data with our mobile phones and surf the Web with high-end PDAs. In the near future, especially the coming of age of 3G wireless devices, every type of electronic data channel will be used to exchange every type of electronic information. One of the great challenges of the ability to communicate digitally is securing the increased amount of electronic information now exchanged over the network.
Over the last three decades the traditional cryptosystems like DES, DLP, RSA, DSA etc. have thus far been the answer to the wide range of issues that impact modern communication, including the assurance of privacy, the certainty of the transmitter or receiver’s identity and the integrity of the communication[1,2]. Today, these traditional crypto-algorithms which were once considered effective have become in impractical in light of recent technological development of constrained environment devices. These conventional crypto-tech approaches cannot support the new generation of digital communication and information access devices with their low power, small form factor and high performance requirements. The emerging breed of laptops, handhelds, mobile phones, PDAs and wireless devices require a next-generation crypto-security technology.
However, it is important to note that traditional cryptographic algorithms like DLP[3], RSA[4] etc. are not particularly efficient in small form factor, low-power, resource constrained devices, as they require memory intensive power hungry big integer computation co-processor to complete the calculations in a timely manner[1]. Adding such a co-processor significantly raises the cost of manufacture, rendering many devices impractical. The cost of producing a smartcard, for example, is increased by as much as 400% when an additional processor is required[5]. For embedded systems or telecommunications applications characterized by extremely high volumes and a wide variety of devices, many of which have limited computing resources, the trend has been towards alternate crypto-algorithms.
One technology in particular, called Elliptic Curve Cryptography (ECC), has become the cryptography of choice for mobile computing and communications devices due to its size and efficiency benefits. Elliptic curve cipher uses very small keys and is computationally very efficient, which makes it ideal for the smaller, less powerful devices being used today by majority of individuals to access network services. Its efficiency enables constrained, wireless devices to establish secure end-to-end connections. Hence, the server-side crypto-security networks have to be enabled to perform ECC operations for the next generation of wireless devices that use variable parameters in an efficient way to reduce systems cost. In Koblitz[6] and Miller[7], independently proposed the Elliptic Curve Cryptosystem (ECC)-a crypto-algorithm method of utilizing a Discrete Logarithm Problem (DLP) over the points on an elliptic curve. By their proposal, ECC could be used to provide both digital signatures and an encryption scheme. Over the past decade, ECC and later ECDLP (Elliptic Curve Discrete Logarithm Problem)[8,9] has received considerable attention from mathematicians around the world and no significant breakthroughs have been made in determining weaknesses in the algorithm and to-date has weathered umpteen mathematical attacks. Elliptic curve cryptosystems have thereby come to be accepted today as the most viable public-key technology for high-security applications. They are also most suitable for constrained environment devices such as those in which smartcards and personal wireless devices are typically deployed. Over the coming years, there will continue to be a great need for designing and implementing ECC enabled cryptosystems ranging from software, protocols and hardware solutions to secure cutting-edge technologies such as: smartcards, mobile phones, browsers, servers, Radio Frequency Identification (RFID) tags and environmental sensors.
The ECC provides higher strength-per-bit than any other current public-key cryptosystems[10]. If you compare elliptic curves to RSA and DLP you find many advantages: to obtain the same security one can use smaller fields for elliptic curves[11,12]. Therefore, elliptic curves can be implemented easier and faster. Furthermore, because of its higher strength-per-bit, ECCs are being increasingly used in practical applications in embedded systems (e.g., IC card and mobile devices) instead of RSA, which today is the most used public-key cryptosystems. The Elliptic Curve Crypto-schemes are also used for implementing protocols such as EC-digital signature scheme (ECDSA)[13], Diffie-Hellman key exchange scheme[14], EC ElGamal crypto-schemes[15] and so on. Following in the footsteps of DES[16]; ECC in conjunction with advance symmetric algorithm, AES[17], has already been incorporated into a number of key international standards, including ANSI X9.63, IEEE 1363-2000, IETF RFC 3278, ISO 15946-3 and NIST SP 800-56[18]. Further evidence of widespread acceptance are the inclusion of ECC in IPsec, TLS and OpenSSL[19,20]. Adoption into global standards will assist in pushing ECC into wider commercial usage. This integration in to the standard crypto-security systems will greatly enhance the overall usage of the next generation of wireless devices like 3G, which are extremely powerful but must still conserve their power consumption to achieve a longer working battery cycle. This is another advantage for using ECC which uses very small keys and is computationally very efficient which makes it ideal for the smaller, less powerful devices being used today by majority of individuals to access network services. With the commercial-grade implementations of ECC, developers should also expect to see an overall speed increase introduced by computational optimizations.
Today RSA is the powerhouse crypto-security of choice for e-commerce transactions, but its key size must double by the end of this decade to provide the same level security. At this point RSA crypto-technology become an extreme heavyweight for constrained environment devices (Fig. 1). Another factor going against the future of RSA is they are too slow compared to ECC, due to their dependence on computational involving two large prime integers, while the latter does not. The future of Internet security will also be greatly enhanced when they finally switch to elliptic curve based crypto-server security. With ECC smaller key-size requirements and enhanced computational efficiency, IT connectivity providers will be able to utilize fewer crypto-server security for providing secure network connections. Table 1 compares the equivalent security level for some commonly considered cryptographic key sizes.
As ECC becomes more important and more widely used, we foresee the following scenario. Commercial entities such as financial services or online stores running e-business will carry out transaction with users over the wireless conveniently and securely. The servers are required to perform crypto-operations such as signature generation and verification and key exchange. Most of these operations will employ standardized settings such as the NIST recommended elliptic curves[20]. However, there may be users that generate curves themselves, or Certificate Authorities (CA) that issue certificates over non-standardized curves that promise a performance gain. For example, they might want to use a curve defined over GF(2155) as described by Schroeppel et al.[21], a curve over GF(2178) as presented by Schroeppel et al.[22], or curves suited to special field element representations by De Win et al.[23]. There may also be standards which are rarely used and thus do not justify the implementation of a special case and future standards may introduce new curves. Still, a server must be able to handle all requests efficiently to reduce computing time and hence efficiency and cost.
It should be stressed, however, that there are also potential drawbacks associated with ECC from a practical perspective: RSA operations involving public keys (i.e., signature verification or encryption) can be performed with very short keys (Table 2). This leads to very fast operations which are usually faster than the corresponding ECC operations. However, RSA operations with private keys are usually much slower. In addition, the performance advantage for public key will decrease in future as longer bit length will become more common place for both RSA and ECC, (Fig. 1 and Table 1).
| Table 1: | Comparison of the equivalent security level for some commonly used cryptographic key sizes |
 | |
| Table 2: | Comparisons of ECC vs. RSA vs. DH* |
 | |
*Timings were taken on BlackBerry 7230 at 128-bit security level. Timings at a 256-bit security level would show even greater differences between ECC, RSA and DH. **Time was too long to measure[22] | |
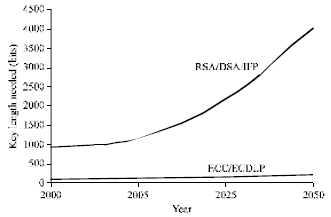 | |
| Fig. 1: | Proposed the minimum key sizes (in bits) to be regarded as safe for RSA and ECC |
In this study we analyze the elliptic curve operations of these ECC protocols and design procedure of the Elliptic Curve Cryptographic defined over binary finite field GF(2m).
GENERAL ELLIPTIC CURVES
Elliptic curve cryptology uses mathematical ideas such as: groups, Abelian groups, operations with groups, fields, operations with fields, elliptic curves and elliptic curve arithmetic using fields and groups. Let k be a field, ![]() its algebraic closure and K* its multiplicative group. An elliptic curve over K will be defined as the set of solution in projective plane
its algebraic closure and K* its multiplicative group. An elliptic curve over K will be defined as the set of solution in projective plane ![]() 2 (
2 (![]() ) of a homogeneous Weierstrass equation of the form:
) of a homogeneous Weierstrass equation of the form:
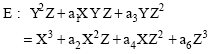 | (1) |
With a1, a2, a3, a4, a6 ∈ K. This equation is referred to as long Weierstrass form. Such a curve should be non-supersingular in the sense that, if the equation is written in the form F(X, Y, Z) = 0, then the partial derivatives of the curve equation ∂F/∂X, ∂F/∂Y and ∂F/∂Z should not vanish simultaneously at any point on the curve.
Let ![]() be a field satisfying K ⊆
be a field satisfying K ⊆ ![]() ⊆
⊆ ![]() . A point(X, Y, Z) on the curve is
. A point(X, Y, Z) on the curve is ![]() -rational if (X, Y, Z) = α
-rational if (X, Y, Z) = α ![]() for some α ∈
for some α ∈ ![]() ,
, ![]() i.e. up to projective equivalence, the coordinates of the point are in
i.e. up to projective equivalence, the coordinates of the point are in ![]() . The set of
. The set of ![]() -rational points on E is denoted by (
-rational points on E is denoted by (![]() ). When the field of definition of the curve, K, is clear from the context, we will refer to
). When the field of definition of the curve, K, is clear from the context, we will refer to ![]() -rational points simply as rational points. The curve has exactly one rational point with coordinate Z equal to zero, namely (0,1,0). This is the point at infinity, which will be denoted by O.
-rational points simply as rational points. The curve has exactly one rational point with coordinate Z equal to zero, namely (0,1,0). This is the point at infinity, which will be denoted by O.
For convenience, we will most often use the affine version of Weierstrass equation, given by:
| (2) |
Where, ai ∈ K. The ![]() -rational points in the affine case are the solutions to E in
-rational points in the affine case are the solutions to E in ![]() 2 and the point at infinity O. For curves over the reals, this point can be thought of as lying infinitely far up the y-axis[8]. We will switch freely between the projective and affine presentations of the curve, denoting the equation in both cases by E. For Z ≠ 0, a projective point (X, Y, Z) satisfying Eq. 1 corresponds to the affine point (X/Z,Y/Z) satisfying Eq. 2.
2 and the point at infinity O. For curves over the reals, this point can be thought of as lying infinitely far up the y-axis[8]. We will switch freely between the projective and affine presentations of the curve, denoting the equation in both cases by E. For Z ≠ 0, a projective point (X, Y, Z) satisfying Eq. 1 corresponds to the affine point (X/Z,Y/Z) satisfying Eq. 2.
Finite field selections: Key in implementation of ECC is selection of elliptic curve groups over the finite fields of the form GF(p) or ![]() p and GF(pm) or
p and GF(pm) or ![]() where, p is prime and m is a positive integer. By definition elliptic curve groups are additive groups. Various finite field can be generated using values of p, m and f(x), where
where, p is prime and m is a positive integer. By definition elliptic curve groups are additive groups. Various finite field can be generated using values of p, m and f(x), where ![]() , fi∈ GF(pm). Also using generic algorithm for different kind of field faster efficiency rate can be achieved.
, fi∈ GF(pm). Also using generic algorithm for different kind of field faster efficiency rate can be achieved.
Field over GF(p) is also known as integer modulo p, even, or odd prime[8]. Using GF(p) will require a coprocessor to perform the modular operation. Hence, obviously the performance with a GF(p) will be lower compared to that over binary field GF(2m). Furthermore, addition of a coprocessor in small form factor devices like smartcard increases the cost by 20 to 40%. Hence, for practical applications finite field of the form ![]() are very important. For such elliptic curves the theory as developed by Rabah[8] has to be modified.
are very important. For such elliptic curves the theory as developed by Rabah[8] has to be modified.
ELLIPTIC CURVE OVER CHARACTERISTIC 2 (BINARY FINITE FIELD), GF(2m)
We now specialize on finite field ![]() q where, q = 2m, m ≥ 1. Elements of the finite field
q where, q = 2m, m ≥ 1. Elements of the finite field ![]() are binary of fixed length m. There are several ways to define arithmetic in this field, but the most common are polynomial representation. Up till now, no experiments have suggested a link between the field representation and the complexity of the resulting elliptic curves. So the choice of representation for the finite field does not appear to affect the security level of the elliptic curves defined over it.
are binary of fixed length m. There are several ways to define arithmetic in this field, but the most common are polynomial representation. Up till now, no experiments have suggested a link between the field representation and the complexity of the resulting elliptic curves. So the choice of representation for the finite field does not appear to affect the security level of the elliptic curves defined over it.
Under these assumptions, a representative for each isomorphism class elliptic curves over ![]() q is given by:
q is given by:
| (3) |
Where, a1 = 1, ![]() and a2 ∈{0, γ} with γ a fixed element in
and a2 ∈{0, γ} with γ a fixed element in ![]() q of trace
q of trace ![]() ( γ) = 1 , where, Trq|2 is the linear trace from
( γ) = 1 , where, Trq|2 is the linear trace from ![]() q to
q to ![]() 2. This function is not directly related to trace of Frobenius and no confusion should arise since they are used in quite different context. In this case, the expression for the j-invariant reduces to
2. This function is not directly related to trace of Frobenius and no confusion should arise since they are used in quite different context. In this case, the expression for the j-invariant reduces to ![]() . In characteristic two, the condition j(E) = 0, i.e., a1 = 0, is equivalent to the curve being supersingular, which is a very special type of curve and is avoided in cryptography. We assume, therefore, that j(E) ≠ 0.
. In characteristic two, the condition j(E) = 0, i.e., a1 = 0, is equivalent to the curve being supersingular, which is a very special type of curve and is avoided in cryptography. We assume, therefore, that j(E) ≠ 0.
The finite field ![]() , called a binary field, can be viewed as a vector space of dimension m over
, called a binary field, can be viewed as a vector space of dimension m over ![]() That is, there exists a set of m elements {e0, e1,…em-1} in
That is, there exists a set of m elements {e0, e1,…em-1} in ![]() such that each
such that each ![]() can be written uniquely in the form
can be written uniquely in the form ![]() where,
where, ![]() i.e., ai = 0 or 1. The set {e0, e1, …em-1} is called a basis of
i.e., ai = 0 or 1. The set {e0, e1, …em-1} is called a basis of ![]() over
over ![]() We can then represent a as a binary vector a = (a0, a1,…am-1). There are many different basis of
We can then represent a as a binary vector a = (a0, a1,…am-1). There are many different basis of ![]() . The most natural basis are, of course, polynomial basis, normal basis and optimal normal basis. In polynomial basis, we just have ei = ti where, t is he fixed complex (or whatever) root of our reduction trinomial : tm + tk + 1. (Note that it is possible to chose another basis, called a normal basis, of the form:
. The most natural basis are, of course, polynomial basis, normal basis and optimal normal basis. In polynomial basis, we just have ei = ti where, t is he fixed complex (or whatever) root of our reduction trinomial : tm + tk + 1. (Note that it is possible to chose another basis, called a normal basis, of the form: ![]() where,
where, ![]() It is well known that such a basis always exists). The most natural basis are, of course, polynomial basis, normal basis and optimal normal basis (Table 3).
It is well known that such a basis always exists). The most natural basis are, of course, polynomial basis, normal basis and optimal normal basis (Table 3).
Optimal extension finite field : Field of ![]() uses p = 2 such that it gives implementer f(x) of form trinomial or polynomial. An alternative representation of
uses p = 2 such that it gives implementer f(x) of form trinomial or polynomial. An alternative representation of ![]() is the Optimal Extension Fields (OEFs). OEFs is an alternative construction to the
is the Optimal Extension Fields (OEFs). OEFs is an alternative construction to the ![]() where, p = 2n ± c, where c is arbitrary positive rational number log2c = n/2. Also p is prime less than but close to the word size of the processor. In addition, m is chosen such that, f(x) = xm-w, is an irreducible. The goal is to select parameters which provide adequate security without incurring excessive computation time.
where, p = 2n ± c, where c is arbitrary positive rational number log2c = n/2. Also p is prime less than but close to the word size of the processor. In addition, m is chosen such that, f(x) = xm-w, is an irreducible. The goal is to select parameters which provide adequate security without incurring excessive computation time.
Lenstra and Verheul[24] showed that under certain assumptions, 925-bit RSA and DSA systems may be considered equivalent in security to a 132-bit ECC system. The field GF((28-17)17), for example, a security level of 134-bits which is far more secure than 512-bit RSA system which has been popular for smartcard applications. Optimal Extension Fields (OEF) are computationally more efficient than other field types offering roughly the same level of security[25]. Table 4 displays three fields of similar field order, which implies a similar security strength of the cryptosystem based on these fields[26]. The third column denotes the number of cycles for one field multiplication which is the crucial operation determing the efficiency of the system. One can see that the OEF displayed in the third row performs more efficient than the binary field displayed in the first row.
Composite extension finite fields and subfields: When m is a composite number, m = rs, then the composite extension finite field GF(2m) can be considered an extension field of degree s over finite field GF(2r). The finite field GF(2r) is called a subfield of GF(2m). The elliptic curve over a subfield is also used in computing the order of an elliptic curve over a composite extension finite field using Hasse-Weil’s theorem[8]. We can also represent elements in a composite extension finite field over its subfield using either one of the two basis discussed earlier.
We should point out that the finite field GF((2r)s) is isomorphic to the finite field GF(2m), but their field operations (additions and multiplications) are different depending on the irreducible field polynomials, f(x) of GF((2r)s) over GF(2r) and GF(2r) over GF(2). It also depends on the possible factorizations of m (other than factors r and s). The choice of those field polynomials are essential to determine the algorithmic complexity of arithmetic operation of GF((2r)s). However, a recent attack on ECCs over composite fields makes them inappropriate for use in practice[25].
| Table 3: | Comparisons of different finite fields for implementing ECC |
 | |
| Table 4: | ECC field performance |
 | |
ARITHMETIC OVER FINITE FIELD GF(2m) USING POLYNOMIAL BASIS EPRESENTATION
A good understanding of the complexity of the mathematics in the field ![]() is necessary to appreciate the difficulty of solving equations of elliptic curves defined over this field[8,9]. The elements of the finite field
is necessary to appreciate the difficulty of solving equations of elliptic curves defined over this field[8,9]. The elements of the finite field ![]() are binary strings of fixed length m. As indicated above there are many ways to construct a finite field with a prime power number elements, but the most common are polynomial representation, normal and optimal normal representation.
are binary strings of fixed length m. As indicated above there are many ways to construct a finite field with a prime power number elements, but the most common are polynomial representation, normal and optimal normal representation.
The polynomial basis representation: Polynomial basis representation can be used to implement addition, multiplication, division and remainder or modulus operation. This being the case, implementation presented in this section, uses field polynomial representation because of its relatively easy arithmetic operations.
Let ![]() where, each
where, each ![]() . We call f(x) the reduction polynomial (or sometimes, field polynomial). The polynomial f(x) must be irreducible; that is, it cannot be factored into two polynomials over
. We call f(x) the reduction polynomial (or sometimes, field polynomial). The polynomial f(x) must be irreducible; that is, it cannot be factored into two polynomials over ![]() , each of degree less than m. In polynomial basis form, the elements of
, each of degree less than m. In polynomial basis form, the elements of ![]() are treated as polynomials of degree m, with the individual bits representing coefficients in
are treated as polynomials of degree m, with the individual bits representing coefficients in ![]() of each term. So elements are of the form:
of each term. So elements are of the form:
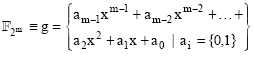 | (4) |
These elements ![]() can be written in binary strings or vector form as (am-1…a1,a0) of length m.
can be written in binary strings or vector form as (am-1…a1,a0) of length m. ![]() has 2m elements, i.e.,
has 2m elements, i.e., ![]() Particularly, we can write the zero element 0 = (0, 0,…0) and the multiplicative identity 1 = (0, 0, …0, 1).
Particularly, we can write the zero element 0 = (0, 0,…0) and the multiplicative identity 1 = (0, 0, …0, 1).
Let ![]() denote the set of all non-zero elements in
denote the set of all non-zero elements in ![]() . The field
. The field ![]() is cyclic, which means: G = {g0, g1, …, gn}where, gn = I, with n = 2m -1 and I is the identity element. Here g ∈ G, where, g ≠ 0, is called a generator (or primitive) element. By definition, this means that any group element can be expressed as a power of g. The multiplicative inverse of an element: a = gi is
is cyclic, which means: G = {g0, g1, …, gn}where, gn = I, with n = 2m -1 and I is the identity element. Here g ∈ G, where, g ≠ 0, is called a generator (or primitive) element. By definition, this means that any group element can be expressed as a power of g. The multiplicative inverse of an element: a = gi is ![]() . This method of representing
. This method of representing ![]() is called a polynomial basis representation.
is called a polynomial basis representation.
Since ![]() is a mathematical ’field’, it has the binary operations of addition and multiplication. Table 5 shows bit-to-binary-to-polynomial representation and their decimal equivalence. Note that the presence of the coefficient is marked by a digit 1 and the absence is marked by a digit zero, 0, e.g g = {a3x3+a2x2+1}, will be written as:(a3a2a1a0) = (1101).
is a mathematical ’field’, it has the binary operations of addition and multiplication. Table 5 shows bit-to-binary-to-polynomial representation and their decimal equivalence. Note that the presence of the coefficient is marked by a digit 1 and the absence is marked by a digit zero, 0, e.g g = {a3x3+a2x2+1}, will be written as:(a3a2a1a0) = (1101).
Irreducible polynomials: A polynomial f(x) is said to be irreducible if we cannot write, f(x) = h(x).u(x), for any polynomials h(x), u(x) of degree strictly less than the degree of f(x). An irreducible polynomial ![]() of degree m over
of degree m over ![]() should satisfy these necessary conditions:
should satisfy these necessary conditions:
| • | The constant term f0 = 1; otherwise, we can factor x out. Hence, from now on we always write the general form as: |
| • | There is an odd number (≥3) of nonzero terms; otherwise, f(x) whose number of nonzero terms is even has a factor (x+1). |
| • | There must be at least one term of odd degree; otherwise, f(x) of all even powers is a square of a polynomial of degree (m/2). |
| • | It is easy to verify this property: If |
| • | The compositions of h(x) and u(x) will give us a few more irreducible polynomials. |
| Table 5: | Implement of binary-to-polynomial basis representation |
 | |
Primitive polynomials: If the period of f(x) is (2m-1), that is the order of the multiplicative subgroup ![]() , then f(x) is called a primitive polynomial. For example, if
, then f(x) is called a primitive polynomial. For example, if ![]() is an irreducible polynomial of degree m over
is an irreducible polynomial of degree m over ![]() and r is a root of f(x) in an extension field of
and r is a root of f(x) in an extension field of ![]() (that is a finite field
(that is a finite field ![]() ), then
), then ![]() are all roots of f(x). Indeed, if f(r) = 0, then for any d, we have
are all roots of f(x). Indeed, if f(r) = 0, then for any d, we have ![]() since fi equals to 0 or 1. Hence:
since fi equals to 0 or 1. Hence:
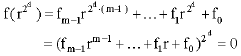 |
Note that all the roots of the polynomial f(x) have the same multiplicative order, that is called the period (or order) of the function f(x).
All roots of a primitive polynomial f(x) are primitive elements of ![]() . For example, the polynomial u(x) = xm +…+ x + 1 divides (xm+1+1). Hence, its period is equal to (m+1) or less and u(x) is not a primitive polynomial of
. For example, the polynomial u(x) = xm +…+ x + 1 divides (xm+1+1). Hence, its period is equal to (m+1) or less and u(x) is not a primitive polynomial of ![]() , unless m = 2.
, unless m = 2.
A primitive polynomial can be built from a primitive element a of a finite field ![]() by the formula:
by the formula:
If another primitive polynomial
is built from a primitive element b, such that ![]() then h(x) ≠ f(x).
then h(x) ≠ f(x).
In other words, each primitive element is a root of only one primitive polynomial of ![]() . In fact, the set of roots of all primitive polynomials for a finite field are exactly all primitive elements in
. In fact, the set of roots of all primitive polynomials for a finite field are exactly all primitive elements in ![]() . Hence, there can be many primitive polynomials for a finite field
. Hence, there can be many primitive polynomials for a finite field ![]() , when m≥3. And in fact, a primitive polynomial cannot be reducible over
, when m≥3. And in fact, a primitive polynomial cannot be reducible over ![]() .
.
Rules for selecting a reduction polynomial
| • | A trinomial over |
| • | A pentanomial over |
ANSI X9.62 specifies the following rules for selecting the reduction polynomial for representing the elements of ![]() [13]:
[13]:
| • | If there exists an irreducible trinomial of degree m over |
| • | If there does not exist an irreducible trinomial of degree m over |
Field addition and multiplication over binary finite field GF(2m): Field elements are added and multiplied as follows:
Field addition (+): Is performed component-wise by XORing (XOR symbol: ⊕, but here for simplicity we will use + instead). Addition in ![]() is
is ![]() where each c=ai+bi over
where each c=ai+bi over ![]() . That is, addition is just the componentwise XOR. In the field
. That is, addition is just the componentwise XOR. In the field ![]() , each element (am-1…a1a0) is its own additive inverse, since (am-1…a1a0)+ (am-1…a1a0)=(0…00), the additive identity. Thus, addition and subtraction are equivalent operations in
, each element (am-1…a1a0) is its own additive inverse, since (am-1…a1a0)+ (am-1…a1a0)=(0…00), the additive identity. Thus, addition and subtraction are equivalent operations in ![]() . Since
. Since ![]() for all binary elements, then g+g = 0 = g-g. So we note that addition and subtraction are equivalent in this field, Fig. 2a on how to perform XOR operation. In hardware, a bit-parallel adder requires m-tuples as in a = (am-1, am-2,…a0). In hardware, a bit-parallel adder requires m XOR gates and addition can be generally computed in one clock cycles.
for all binary elements, then g+g = 0 = g-g. So we note that addition and subtraction are equivalent in this field, Fig. 2a on how to perform XOR operation. In hardware, a bit-parallel adder requires m-tuples as in a = (am-1, am-2,…a0). In hardware, a bit-parallel adder requires m XOR gates and addition can be generally computed in one clock cycles.
Field multiplication (•): Multiplication of field elements in ![]() uses the same shift-and-add algorithm as is used for multiplication of integers, except that the “add” is replaced with “XOR”. This has the virtue that the operation can no longer generate carriers, simplifying the implementation. That is,
uses the same shift-and-add algorithm as is used for multiplication of integers, except that the “add” is replaced with “XOR”. This has the virtue that the operation can no longer generate carriers, simplifying the implementation. That is, ![]() where, the polynomial
where, the polynomial ![]() is the remainder when the product polynomial
is the remainder when the product polynomial ![]() is divided by the polynomial f(x) over
is divided by the polynomial f(x) over ![]() , where, the operation (•) is carried out Fig. 2b. (Note that all polynomial coefficients are reduced modulo 2.)
, where, the operation (•) is carried out Fig. 2b. (Note that all polynomial coefficients are reduced modulo 2.)
Field exponentiation: The exponentiation (am-1…a1a0)e is performed by multiplying together e copies of (am-1…a1a0).
Multiplicative inversion: The rules for doubling an elliptic curve point and for adding two elliptic curve points, involve computing reciprocal, either 1/x or 1/(x1+x2). Multiplicative inversion of elements in a field is usually so slow that people have gone to great lengths to avoid it. Menezes et al.[5] and Beth and Schaefer[27] discuss projective schemes, which use about nine multiplications per elliptic curve step , but use very few reciprocals. An efficient algorithm for computing an inverse of an element in ![]() was proposed by Itoh et al.[28].
was proposed by Itoh et al.[28].
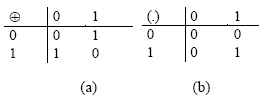 | |
| Fig. 2: | (a) Addition rule and (b) Multiplication rule under finite field, |
Rule to perform multiplicative inverse: We need to discuss also some methods of computing the inverse of a non-zero element. This operation obviously has an important role in field arithmetic, these are:
| • | The general method is using this identity: |
| Odd: 2m-1 -1 = (2(m-1)/2-1)×(2(m-1)/2 + 1) and Even: 2m-1 -1 = 2×(2(m-2)/2 - 1)×(2(m-2)/2 + 1) |
These formulae yield an algorithm for computing inverse by factorization of the exponent. Consider the field, GF(2155):
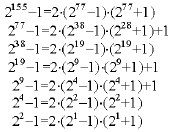 |
It requires 10 multiplications to compute an inverse in GF(2155). In general, the method requires: ![]() field multiplications.
field multiplications.
| • | Alternatively, using the extended Euclidean algorithm: finding polynomials u(x) and v(x) such that ged(f(x), a(x)) = f(x)×u(x)+a(x)×v(x). When ged(f(x), a(x)) = 1, we can write 1 º a(x)×v(x)(mod f(x)). In other words, the polynomial v(x) is the inverse of a(x), modulo f(x). |
Squaring: In particular, the squaring operation of a polynomial ![]() that is performed in modulo 2 is in fact a linear operation, i.e.,:
that is performed in modulo 2 is in fact a linear operation, i.e.,:
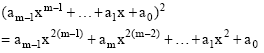 | (5) |
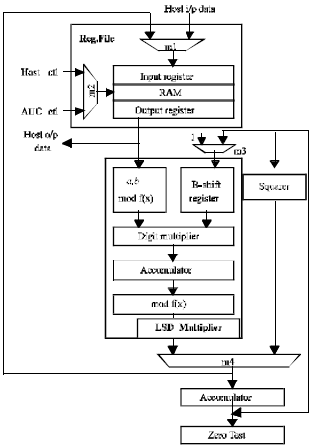
In terms of bit strings, we write: (am-1…a1a0) = (a2(m-1), 0, a2(m-2), 0 ,…0, a1, 0, a0). Then we reduce the resulting polynomial by modulo f(x). In hardware, a bit-parallel realization of this squarer requires at most (r-1)(m-1) gates[29,30], where, r represents the number of non-zero coefficients of the polynomial when implemented using Elliptic Curve Processor (ECP) architecture (Fig. 3 and 4) field arithmetic module. The components are the Main Controller (MC), the Arithmetic Unit Controller (AUC) and Arithmetic Unit (AU). The MC is the ECP’s main controller which performs the computation of the scalar multiplication, kP.
The AUC controls the AU and performs the computation of point additions, point doublings and coordinate conversions. The AU also performs GF(2m) field additions, squares, multiplications and inverses under AUC control[31].
Orlando and Paar[31] proposed a design for the standard basis field representation and it is based on the transformation from squaring operation into an addition and a multiplication by a constant that depends only on the field polynomial. For example, squaring a polynomial in a modulo 2 field is a linear operations. In the formula for squaring a binomial, (a+b)2 =a2+2ab+b2, the cross-term vanishes modulo 2 and the square reduces to a2+b2. Consequently, we can square a sum by squaring the individual terms. For example, (u3+u+1)2 = u6+u2+1.
In terms of bitstrings, to square a polynomial, we spread it out by interleaving a 0 bit between each polynomial bit. For example, x3+x+1 is represented as 1011 and the square (x3)2+x2+12 = x6+x2+1 is represented by 1000101 (Table 5). Sadly, computer manufacturers have largely ignored the need for an instruction to carry out this operation; nonetheless, it can be done quickly using table lookup to convert each byte to its 15-bit square. The squared polynomial is then reduced modulo f(x). Squaring is so much faster than regular multiplication that it can be ignored in rough comparisons of the timings.
THE ELLIPTIC CURVE OVER FINITE FIELD GF(2m)
Elements of the field ![]() are m-bit string. The rules in
are m-bit string. The rules in ![]() can be defined by either polynomial representation and by normal or optimal normal basis representation as started earlier. Let
can be defined by either polynomial representation and by normal or optimal normal basis representation as started earlier. Let ![]() be a characteristic 2 finite field and let
be a characteristic 2 finite field and let ![]() satisfy b≠0 in
satisfy b≠0 in ![]() . Then an elliptic curve
. Then an elliptic curve ![]() over
over ![]() defined by the parameters
defined by the parameters ![]() consists of the set of solutions or points P = (x, y) for
consists of the set of solutions or points P = (x, y) for ![]() to the equation:
to the equation:
| (6) |
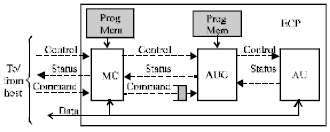 | |
| Fig. 3: | Elliptic Curve Processor (ECP) architecture |
 | |
| Fig. 4: | Elliptic curve Arithmetic Unit (AU) |
together with an extra point O called the point at infinity. (Here the only elliptic curves over ![]() of interest are non-supersingular elliptic curves[27].) Since
of interest are non-supersingular elliptic curves[27].) Since ![]() operates on the bit strings, computers can perform arithmetic in this field very efficiently. The number of points on
operates on the bit strings, computers can perform arithmetic in this field very efficiently. The number of points on ![]() is denoted by
is denoted by ![]() .
.
Counting points on elliptic curves: A user of ECC will be interested to know the structure of the group, especially he would like to know the number of the points, ![]() . If he knows
. If he knows ![]() he knows whether the Pohlig-Hellman-attack can be applied. It is
he knows whether the Pohlig-Hellman-attack can be applied. It is
impossible to write down all the points for large q. But it is not necessary at all. The formula of Hesse-Weil can be applied, which reduces the amount of work enormously, which states that if E is an elliptic curve over ![]() [8,32], then, then:
[8,32], then, then:
| (7) |
![]() such that
such that ![]() is called the trace of the curve.
is called the trace of the curve.
Note that E (![]() ) (where, q = 2m) is called the group of rational points i.e., points that are rational over the ground field
) (where, q = 2m) is called the group of rational points i.e., points that are rational over the ground field ![]() . Not to be confused with E(Q)! the knowledge of the rational points on the curve is essential to cryptosystems because we often desire curves E with a large prime dividing
. Not to be confused with E(Q)! the knowledge of the rational points on the curve is essential to cryptosystems because we often desire curves E with a large prime dividing ![]() . So we can either construct curves with the right properties (like
. So we can either construct curves with the right properties (like ![]() ) containing a large prime) or generate curves randomly and check if they have the desired properties. Hence, efficient computation of
) containing a large prime) or generate curves randomly and check if they have the desired properties. Hence, efficient computation of ![]() is an important question. Both approaches are useful depending on the application. For example EC factoring algorithms search for curves where the number to be factored, decomposes smoothly.
is an important question. Both approaches are useful depending on the application. For example EC factoring algorithms search for curves where the number to be factored, decomposes smoothly.
The order n of a point P ≠ O on an elliptic curve is a positive integer such that nP = O and mP≠O for any integer m such that 1 ≤ m < n. The order n of a point must divide the order N of the elliptic curve. In fact, it is true for any group. If the elliptic curve order N = ![]() is a prime number, then the group is cyclic and obviously all points except the point at infinity O are of order N.
is a prime number, then the group is cyclic and obviously all points except the point at infinity O are of order N.
Elliptic curve arithmetic over finite field ![]() : It is again as is the case with elliptic curve over
: It is again as is the case with elliptic curve over ![]() [8], there is a chord-and-tangent rule for adding point on an elliptic curve E(
[8], there is a chord-and-tangent rule for adding point on an elliptic curve E(![]() )to give a third elliptic point. Together with this addition operation, the set of points on E(
)to give a third elliptic point. Together with this addition operation, the set of points on E(![]() ) forms a group with O serving as its identity.
) forms a group with O serving as its identity.
The algebraic formula for the addition of points and the double of a point are specified as follows:
| • | Rule to add the point at infinity to itself: O+O=O |
| • | Rule to add the point at infinity to any other point: |
| • | Rule to add two points with the same x-coordinates when the points are either distinct or have x-coordinate 0: (x, y)+(x, x+y)=O for all (x, y) ∈ E( |
| • | Rule to add a point to itself (double a point): Let |
and
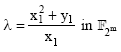 | (8) |
| • | Rule to add two points with different x-coordinates: Again let |
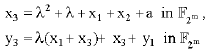 |
and
| (9) |
In either case, when P1+P2 (doubling) and P1 ≠ P2 (point addition), major operations are field multiplication and field inversion. (Squaring and field addition are enough ignorable because of its less computation time.) From these formulas of point addition or doubling, we can determine the number of field operations required for each kind of elliptic curve operation. We see that an addition step usually requires eight additions, two multiplications, one squaring, three reductions mod f(x) and one inversion. A Doubling step usually requires four additions, two multiplications, two squaring, four reductions mod f(x) and one inversion. A Negation step requires one addition. The important contributors to the run time are the multiplications and inversions[28,33]. Just as modular exponentiation determines the efficiency of RSA cryptographic systems[1,4], scalar multiplication dominates the execution time of ECC systems. In all the protocols that are fundamental implementation of ECC, say ECDH, ECDSA, ECAES etc. the most time consuming part of the computations are scalar multiplications[33]. Elliptic curves have some properties that allow optimization of scalar multiplications. Thus, far the efficiency of the finite field arithmetic, especially multiplication, determines the overall efficiency of the elliptic curve cryptosystem.
THE FINITE FIELD GF(24) USING POLYNOMIAL BASIS REPRESENTATION
Let us consider the elliptic curve defined over ![]() which from Eq. 6, we have a = g4 and b = g0 = 1 is given by:
which from Eq. 6, we have a = g4 and b = g0 = 1 is given by:
| (10) |
| Table 6: | 16 elements of |
 | |
| Table 7: | Powers of g using the element g = (0010) as the generator, including the elements of |
Note that b ≠ 0, so E is indeed an elliptic curve. ![]() is constructed using the primitive irreducible polynomial f(x) = x4+x+1 and a root g. The set of points on E(
is constructed using the primitive irreducible polynomial f(x) = x4+x+1 and a root g. The set of points on E(![]() ) forms an abelian group under this addition rule. Notice that the addition rule can always be computed efficiently using simple field arithmetic. The element g = x = (0010) (i.e., g = x(mod f(x)), is a root of f(x) in
) forms an abelian group under this addition rule. Notice that the addition rule can always be computed efficiently using simple field arithmetic. The element g = x = (0010) (i.e., g = x(mod f(x)), is a root of f(x) in ![]() ) is a generator of
) is a generator of ![]() since the number of elements
since the number of elements ![]() and it is cyclic, the powers of g obtained are (Table 6).
and it is cyclic, the powers of g obtained are (Table 6).
Note that all the 15 non-trivial powers of g are primitive elements of the multiplicative subgroup ![]() . The following are sample calculations to demonstrate the property of
. The following are sample calculations to demonstrate the property of ![]() :
:
Addition: (0110)+(0101) = (0011).
Multiplication:
(1101)×(1001) = (x3+x2 +1)×(x3+1) mod f(x)
= x6+x5 +2x3 +x2 +1 mod f(x)
= x6+x5 +x2 +1 mod f(x)
(coefficients are reduced modulo 2)
=(x4+x+1)×(x2+x)+(x3+x2+x+1) mod f(x)
= x3+x2 +x+1 = (1111)
Exponentiation: To compute (0010)5, first find (0010)2: ⇒ (0010)(0010)⇒ xx(mod f(x)) ⇒ (x4+x+1)(0)+(x2) modf(x) ⇒ x2 ⇒ (0100)
Then: (0010)4⇒ (0010)2(0010)2 ⇒ (0100)(0100) ⇒ x2x2 mod f(x) ⇒ (x4+x+1)(1)+(x+1) mod f(x) ⇒ (x+1) ⇒ (0011) ⇒ (x+1) ⇒ (0011)
Finally: (0010)5 ⇒ (0010)4×(0010)⇒ (0011)×(0010) ⇒ (x+1), (x2+x) mod f(x) ⇒ (x4+x+1)(0) + (x2+x) mod f(x) ⇒ x2+x ⇒ (0110)
Multiplicative inversion: Rule to perform multiplicative inverse: There exists at least one element g in ![]() such that all non-zero elements in
such that all non-zero elements in ![]() can be expressed as a power of g. Such an element g is called a generator of
can be expressed as a power of g. Such an element g is called a generator of ![]() . The multiplicative inverse of an element a = gi is
. The multiplicative inverse of an element a = gi is ![]() . The element g = (0010) is a generator for the field. The powers of g are listed in Table 7. The multiplicative identity for the field is g0 = (0001). The multiplicative inverse of g7 = (1011) is g-7mod15 = g8mod15 = (0101). To verify this, we see that:
. The element g = (0010) is a generator for the field. The powers of g are listed in Table 7. The multiplicative identity for the field is g0 = (0001). The multiplicative inverse of g7 = (1011) is g-7mod15 = g8mod15 = (0101). To verify this, we see that:
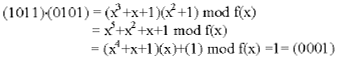 |
Which is the multiplicative identity.
Table 7 shows the use of generator notation (ge) rather than bit notation, as used in the examples above. Also, using generator notation allows multiplication without reference to the irreducible polynomial f(x) = x4+x+1. In a true cryptographic application, the parameter m must be large enough to preclude the efficient generation of such a table otherwise the cryptosystem can be broken. In today’s practice, m = 163 is a minimum suitable choice.
TRACE OF A FINITE FIELD ELEMENT
Trace of an element a is a linear mapping ![]() defined by:
defined by:
Basic properties: Tr(ap) = Tr(a) and Tr(a+b) = Tr(a)+Tr(b) and more generally:
Tr(v×a) = v×Tr(a) for ![]()
When p = 2, Tr(0) = 0 and Tr(1) = 1 if m is odd and Tr(1) = 0 if m is even. These properties can be checked easily from definition and the equality formula for finite fields of characteristic p: (a+b)p = ap+bp for all ![]() , with following properties:
, with following properties:
| • | For an element |
| • | For an element |
Properties on order of an elliptic curve: The following are the Properties on Order of an Elliptic Curve:
| • | Let E be a non-supersingular elliptic curve, E: y2+xy = x3+ax2+b, over the finite field |
| • | Let E be a non-supersingular elliptic curve: E: y2+xy = x3+ax2+b, over the finite field |
| • | The elliptic curve: E: y2 = x3+x2, over a prime finite field |
Example:
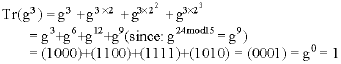 |
Then Tr(gi) = 1, when i = 3, 6, 7, 9, 11, 12, 13 and 14; and Tr(gi) = 0, if otherwise; implemented using trinomial basis notation.
We can verify that two self-dual basis for the finite field ![]() are: {g3, g7, g12, g13} and {g6, g9, g11, g14}. For example: Tr(g7x2) = 1, Tr(g7g3) = Tr(g10) = 0 They are not normal basis. The above trinomial basis is not a dual basis since we have Tr(1) = 0. Now define
are: {g3, g7, g12, g13} and {g6, g9, g11, g14}. For example: Tr(g7x2) = 1, Tr(g7g3) = Tr(g10) = 0 They are not normal basis. The above trinomial basis is not a dual basis since we have Tr(1) = 0. Now define ![]() Then the permutation {1, g, g2, g3} is its dual basis with respect to the linear function h(•).
Then the permutation {1, g, g2, g3} is its dual basis with respect to the linear function h(•).
In fact, there are seven other elements of ![]() using trinomial basis: {1, g, g2, g3} multiplicative subgroup
using trinomial basis: {1, g, g2, g3} multiplicative subgroup ![]() . They are: g2, g4, g7, g11, g13 and g14. The polynomial f(x) = x4+x+1 is primitive and its roots are: g, g2, g4 and g8. The only other primitive polynomial for the finite field
. They are: g2, g4, g7, g11, g13 and g14. The polynomial f(x) = x4+x+1 is primitive and its roots are: g, g2, g4 and g8. The only other primitive polynomial for the finite field ![]() is:
is:
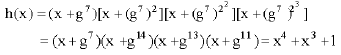 |
Here’s an example using ![]() with generator notation to show that the point (g3,g8) satisfy Eq. 10 over
with generator notation to show that the point (g3,g8) satisfy Eq. 10 over ![]() , i.e.
, i.e.
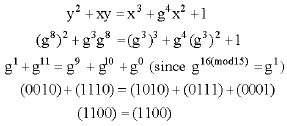 |
Other than the simple integer multiplication of exponents, XOR is the only other operation required. All the fifteen points which satisfy Eq. 10 are as follows:
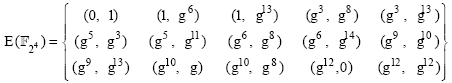 | (11) |
 | (12) |
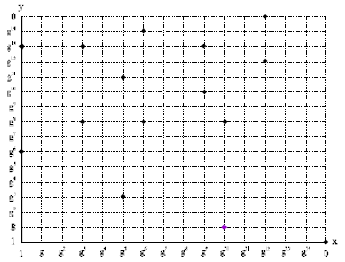 | |
| Fig. 5: | Elliptic curve E: y2+xy = x3+g4x2+1 defined over |
Figure 5 shows the graphical representation of all the points which satisfy Eq. 11. For a given point P = (xp, yp), xp and yp are called the x and y coordinates of P, respectively. We now discuss efficient algorithms to expedite implementation procedures in elliptic curve cryptosystems over binary finite field, ![]() .
.
ALGORITHM FOR ELLIPTIC CURVE SCALAR MULTIPLICATION OVER BINARY FINITE FIELD
Cryptographic schemes based on ECC rely on scalar multiplication of elliptic curve points as demonstrated above. As before given an integer k and a point ![]() , scalar multiplication is the process of adding P to itself k times. The result of this scalar multiplication is denoted by Q = kP = P+P+…+P (k-summands). Here P is a fixed point that generates a large subgroup of (
, scalar multiplication is the process of adding P to itself k times. The result of this scalar multiplication is denoted by Q = kP = P+P+…+P (k-summands). Here P is a fixed point that generates a large subgroup of (![]() ).
).
Let P = (g12, g12) be the generator of E(![]() ) , which we use for scalar multiplication to determine all the points using Eq. 8 and 9 as follows:
) , which we use for scalar multiplication to determine all the points using Eq. 8 and 9 as follows:
Let P = (x1, y1) = (g12, g12). Then 2P = P+P = (x3, y3) is computed as follows:
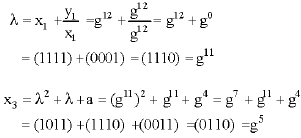 |
and
Hence, 2P = (g5, g11).
Let ![]() and
and ![]() . Then
. Then ![]() is computed as follows:
is computed as follows:
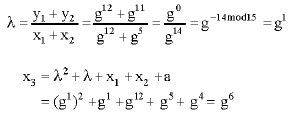 |
and
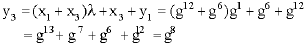 |
Hence, P+Q º P+2P = 3P = (g6, g8). Using the above two operations, we can double point P to obtain 2P. We can then add P to 2P to obtain 3P and continue in this manner until we eventually reach nP = O, the identity point. Since O+P = P, there are n distinct multiples of P. Below we demonstrate this procedure:
Next by again taking P = (g12, g12) and 3P = (g6, g8) we can calculate for 4P = P+3P = (x4, y4) as follows:
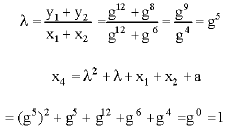 |
and
 |
Hence, P+3P = 4P = (1, g6). Continuing with the similar computational procedure, we can obtain all the points in E(![]() ) , expressed as multiples of P (Table 8).
) , expressed as multiples of P (Table 8).
We note that since point coordinates are elements of ![]() , all arithmetic in the equations above follows the complex rules of
, all arithmetic in the equations above follows the complex rules of ![]() . So the multiplication is done modulo the irreducible polynomial f(x) and the division operation (’/’) in the calculation for λ is actually a field inversion operation. Thus, computing curve points is quite time-consuming for machines to perform and makes it infeasible for a hacker to use a brute-force attack by calculating all multiples of P which is equivalent to solving discrete logarithm in elliptic curve arithmetic, i.e. elliptic curve discrete logarithm problem, ECDLP[8].
. So the multiplication is done modulo the irreducible polynomial f(x) and the division operation (’/’) in the calculation for λ is actually a field inversion operation. Thus, computing curve points is quite time-consuming for machines to perform and makes it infeasible for a hacker to use a brute-force attack by calculating all multiples of P which is equivalent to solving discrete logarithm in elliptic curve arithmetic, i.e. elliptic curve discrete logarithm problem, ECDLP[8].
| Table 8: | Scalar multiplication of elliptic curve points of E( |
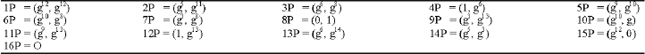 | |
NORMAL AND OPTIMAL NORMAL BASIS REPRESENTATION PRIMITIVE NORMAL BASIS
A normal basis ![]() of the finite field GF(qm) over a finite field
of the finite field GF(qm) over a finite field ![]() where q is any prime power, is called a primitive normal basis if β is a primitive root of the multiplicative subgroup GF(qm)*. According to the theorem by Lenstra and Schoof[36] for every prime power q > 1 and every positive integer m, there exists a primitive normal basis of finite field GF(qm) over
where q is any prime power, is called a primitive normal basis if β is a primitive root of the multiplicative subgroup GF(qm)*. According to the theorem by Lenstra and Schoof[36] for every prime power q > 1 and every positive integer m, there exists a primitive normal basis of finite field GF(qm) over ![]() .
.
Normal basis representation: Normal basis are not special only for finite fields of characteristic 2. More generally, the field ![]() can be viewed as a vector space of dimension m over
can be viewed as a vector space of dimension m over ![]() . That is, there exists a set of m elements g0, g1,.., gm-1 in
. That is, there exists a set of m elements g0, g1,.., gm-1 in ![]() such that each
such that each ![]() can be written uniquely in the form:
can be written uniquely in the form:
where,
We can then represent g as the 0-1 vector (a0a1…am-1). Addition of the field elements is performed by bitwise XOR-ring the vector representation
In fact, they are defined for any finite field ![]() where, q is a prime power. A normal basis of
where, q is a prime power. A normal basis of ![]() over
over ![]() is a basis of the form:
is a basis of the form: ![]() , where,
, where, ![]() . Such a basis always exists. Then g = (a0, a1,…, am-1) will represent the element:
. Such a basis always exists. Then g = (a0, a1,…, am-1) will represent the element: ![]() By convention, the ordering of bits in normal basis representation is different from that in polynomial basis representation. Particularly, we can write the zero element 0= (0,0,…,0) and multiplicative identity 1 = (1,1,…,1).
By convention, the ordering of bits in normal basis representation is different from that in polynomial basis representation. Particularly, we can write the zero element 0= (0,0,…,0) and multiplicative identity 1 = (1,1,…,1).
Addition of field elements in normal basis is performed by bitwise XOR-ing the vector representations. However, the most important property of a normal basis is that the square of a field element can be computed easily and implemented efficiently on hardware by just a right 1-cyclic shift on the register. Indeed, given an element g = (a0,a1,…,am-1) represented in a normal basis, we have:
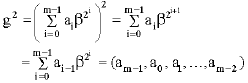 |
With indices reduced modulo m. Then for any integer s, 1 ≤ s ≤ m-1, the 2s-th power of element g can be computed quickly by a right s-cyclic shift. That is ![]() . We can verify again the relationship:
. We can verify again the relationship: ![]() . Similarly, the square root of g can be computed simply by left 1-cyclic shift: g1/2 = (a1, a2, …,am-1, a0). This is useful for recovering points when using the point compression technique for embedding messages for encryption. Hence, a normal basis representation over
. Similarly, the square root of g can be computed simply by left 1-cyclic shift: g1/2 = (a1, a2, …,am-1, a0). This is useful for recovering points when using the point compression technique for embedding messages for encryption. Hence, a normal basis representation over ![]() is advantageous because squaring a field element can then be accomplished by a simple rotation of the vector representation, an operation that is easily implemented in hardware.
is advantageous because squaring a field element can then be accomplished by a simple rotation of the vector representation, an operation that is easily implemented in hardware.
Multiplication in a normal basis: Take, for example, the product C=AB is given by:
Since ![]() is also an element in
is also an element in ![]() , it can be expressed as:
, it can be expressed as:
Where, ![]() . This yields a formulae
. This yields a formulae
![]() for
for ![]()
We also notice that:
Which implies that:
Thus, we have a formula for Cr as:
This formula has remarkable properties. Consider a circuit built for computing C0, which receives the inputs as (in this order):
Uses the formulae to compute:
The same circuit can be used to compute C1:
Unfortunately, as can be seen above multiplication in a normal basis is somehow complicated. Fortunately, multiplication can be easily implemented in hardware when the normal basis used is of a special type called an optimal normal basis[37], which appear to give the most efficient implementation of field arithmetic (with respect to speed and complexity of hardware architecture).
Current implementation of elliptic curves: The algebraic representation of elliptic curves in ![]() is far more efficient than the geometric representation when computing group operations. However, even the simplified algebraic representation of
is far more efficient than the geometric representation when computing group operations. However, even the simplified algebraic representation of ![]() is more than a simple computer can handle in reasonable time. It is possible to represent an elliptic curve in
is more than a simple computer can handle in reasonable time. It is possible to represent an elliptic curve in ![]() so that multiplication can be performed by a few simple linear equations and exponentiation by a left bit rotation. This representation is based on a linear algebraic representation and is called the optimal normal basis representation - a less insightful way to construct the field
so that multiplication can be performed by a few simple linear equations and exponentiation by a left bit rotation. This representation is based on a linear algebraic representation and is called the optimal normal basis representation - a less insightful way to construct the field ![]() , but is computational nicer and easy handling by computers.
, but is computational nicer and easy handling by computers.
Optimal normal basis representation: For many values of m, the finite field ![]() has an optimal basis representation as well as the polynomial representation described above. An optimal basis gives an alternative way of defining multiplication on the elements of a field. While optimal normal basis multiplication is less insightful than polynomial multiplication, it is in practice much more efficient. Further information on
has an optimal basis representation as well as the polynomial representation described above. An optimal basis gives an alternative way of defining multiplication on the elements of a field. While optimal normal basis multiplication is less insightful than polynomial multiplication, it is in practice much more efficient. Further information on ![]() using an optimal basis representation also given by Ron et al.[38].
using an optimal basis representation also given by Ron et al.[38].
Construction of optimal normal basis representation: Optimal normal basis representation (ONB) can be used for a large number of values of m in ![]() . This representation views field elements as linear combinations of the basis matrix for the field. The value of m determines whether a Type I or Type II representation will be used. The determination of the optimal normal basis is as follows:
. This representation views field elements as linear combinations of the basis matrix for the field. The value of m determines whether a Type I or Type II representation will be used. The determination of the optimal normal basis is as follows:
If ![]() has only a Type I representation, then define f(x) = xm+xm-1+xm-2+…+x2+x+1. Otherwise, define f(x) by the recursive formula (Type II):
has only a Type I representation, then define f(x) = xm+xm-1+xm-2+…+x2+x+1. Otherwise, define f(x) by the recursive formula (Type II):
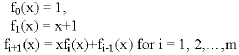 |
Note that f will be reduced in every iteration and will have coefficients in ![]() . The set of polynomials
. The set of polynomials ![]() form a basis of
form a basis of ![]() over
over ![]() , called a normal basis. Form A, a mxm matrix, where each row i is the bit string of length m corresponding to,
, called a normal basis. Form A, a mxm matrix, where each row i is the bit string of length m corresponding to, ![]() . Find Aˉ1.
. Find Aˉ1.
Next construct ![]() , a m x m matrix, where each row i is the bit string of length m corresponding to,
, a m x m matrix, where each row i is the bit string of length m corresponding to, ![]() . Compute T =
. Compute T = ![]() .Tˉ1 . Determine the product terms, Lij = T(j-i,-1), for: i, j = 0, 1,…,m-1. These product terms specify the set of equations by which to perform all operations in
.Tˉ1 . Determine the product terms, Lij = T(j-i,-1), for: i, j = 0, 1,…,m-1. These product terms specify the set of equations by which to perform all operations in ![]() .
.
The generation of the optimal normal basis will be clearer with an example. (Field addition is done as is the case with polynomial basis.) However, for field multiplication let’s consider again our field ![]() , which has a Type I ONB so that: f(x)=x4+x3+x2+x+1. Thus, {x, x2, x4, x8} forms a basis for
, which has a Type I ONB so that: f(x)=x4+x3+x2+x+1. Thus, {x, x2, x4, x8} forms a basis for ![]() over
over ![]() .
.
Construct A as:
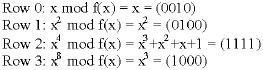 |
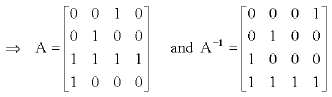 |
Construct T as:
| Row 0: | v = x×x mod f(x) = x2 = (0100) |
| Row 1: | v = x×x2 mod f(x) = x3 = (0100) |
| Row 2: | v = x×x4 mod f(x) = x5 mod f(x) = 1 = (0001) |
| Row 3: | v = x×x8 mod f(x) = x9 mod f(x) = x3+x2+x = (1111) |
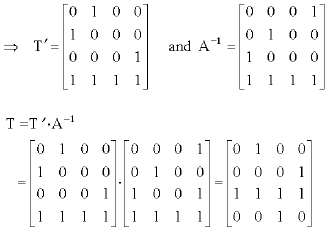 |
Finally, the Lij terms which are 1 are: L0,2, L1,2, L1,3, L2,0, L2,1, L3,1 and L3,3,
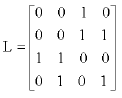 |
How do we use L to define operations in ![]() ? Recall that {x, x2, x4, x8}spans
? Recall that {x, x2, x4, x8}spans ![]() and L is a optimal normal basis for
and L is a optimal normal basis for ![]() . We will write a general formula for multiplication in
. We will write a general formula for multiplication in ![]() :
:
Let A×B = C = (a0a1a2a3)×(b0b1b2b3) = (c0c1c2c3), all in ![]() . Write (a0a1a2a3) and (b0b1b2b3) in terms of the basis {x, x2, x4, x8}, i.e.,
. Write (a0a1a2a3) and (b0b1b2b3) in terms of the basis {x, x2, x4, x8}, i.e.,
 |
Where, each squaring results in a cyclic shifts.
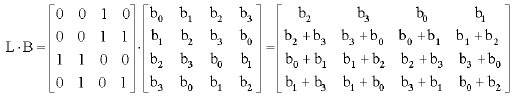 |
The elements of C are the inner products of the corresponding rows and columns of A and B:
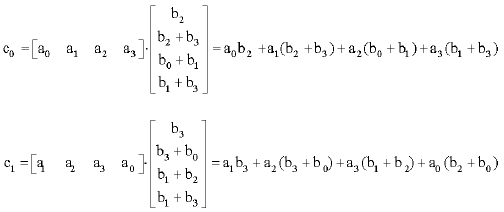 |
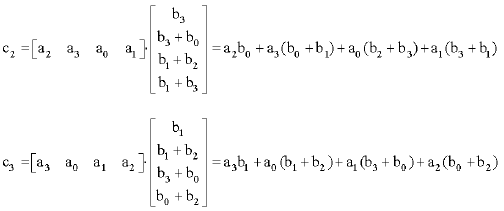 |
With these definitions of addition and multiplication, the 16 binary 4-tuples form a field, although this fact is not obvious.
Note:
| • | The multiplicative identity is (1111) (cf. polynomial basis which was (0001)) |
| • | Notice that: (a0a1a2a3)×(a0a1a2a3) = (a0a1a2a3)2 = (a3a0a1a2) and so the square of a field element is simply a right cyclic shift of its vector representation. |
| • | The formula for c1 in the multiplication can be obtained by adding a 1 to each subscript in the formula for c0 (where the subscripts are reduced modulo 4). The formula for c2 can be obtained by adding 2 to each subscript in the formula for c0 and reducing the formula modulo 4. The formula for c3 can likewise be obtained. |
| • | From the preceding remark we see that a circuit to compute c0 from (a0a1a2a3) and (b0b1b2b3) can be used to compute c1 by applying (a0a1a2a3) and (b0b1b2b3) to it. Similarly, c2 and c3 can be computed by shifting to the left input vectors. |
Thus: (a0a1a2a3)×(b0b1b2b3) = (c0c1c2c3), is implemented as follows:
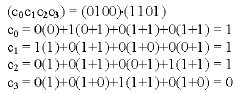 |
and
| (0100).(1101) = (1100) |
Also,
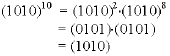 |
and
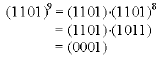 |
Once the multiplication algorithms are computed, they need not be recomputed ever again. The optimal normal basis greatly simplifies multiplication in ![]() , but there is an even greater benefit. The square of any field element is computed to the left cyclic shift of that element, a trivial operation!
, but there is an even greater benefit. The square of any field element is computed to the left cyclic shift of that element, a trivial operation!
Additionally, since an element has a cycle of length m, we have the following consequence as by example:
| (0010)161= (0010)161(mod 4) . (0010)1 = (0010) |
Exponentiation can be simplified and reduced! Consider the finite field ![]() using a normal basis. The reduction polynomial is f(x) = x4+x+1, which you may recall is a primitive polynomial. The optimal normal basis of Type II consists of four polynomials: x, x2, x4 and x8(mod f(x)). A generator for non-zero elements of multiplicative subgroup
using a normal basis. The reduction polynomial is f(x) = x4+x+1, which you may recall is a primitive polynomial. The optimal normal basis of Type II consists of four polynomials: x, x2, x4 and x8(mod f(x)). A generator for non-zero elements of multiplicative subgroup ![]() is chosen to be g = x(mod f(x))
is chosen to be g = x(mod f(x))
In this representation ![]() can be generated by the powers of g = (1100). We can write them explicitly in the Table 9, where:
can be generated by the powers of g = (1100). We can write them explicitly in the Table 9, where:
| (a0, a1, a2, a3) = a0x+a1x2+a2x4+a3x8(mod f(x)) |
For instance, 1 = (1111) = x + x2 + x4 + x8. (All polynomials of modulo f(x) and reduced modulo 2.) We can compute the following intermediate terms and the next repeated squares of each term (by simple right shifts). For example:
x5 = x2 + x = x + x4 = (1010) and x10(0101)
x9 = x3 + 2×x2 + x = x3 + x = x = (1000)
x12 = x3 + 3×x2 + 3.x + 1 = x3 + x2 + x + 1 = x8 = (0001)
Arithmetic in the finite field ![]() can be performed efficiently both in hardware and in software when the field elements are represented with respect to an optimal normal basis.
can be performed efficiently both in hardware and in software when the field elements are represented with respect to an optimal normal basis.
| Table 9: | Powers of g using the element g=(1100) as the generator. This method of representation is called optimal normal basis representation, of Type II (g, g2, g4, g8) |
| Table 10: | Scalar multiplication of elliptic curve points of |
 | |
Since we have demonstrated an example of elliptic curve over ![]() using polynomial basis representation, here we will now give an illustration using optimal normal basis representation. Consider the field
using polynomial basis representation, here we will now give an illustration using optimal normal basis representation. Consider the field ![]() where the elements are the set of all binary 4-tuples with multiplication given by the formulae. Recall that g = (1100) is a generator for the non-zero elements and (1111) is the multiplicative identify.
where the elements are the set of all binary 4-tuples with multiplication given by the formulae. Recall that g = (1100) is a generator for the non-zero elements and (1111) is the multiplicative identify.
Consider the non-supersingular curves over ![]() defined by the equation:
defined by the equation:
| E: y2+xy = x3+g3 |
(Note that to be absolutely precise with our notation, we should write this equation as:
| (1111)y2+(1111)xy = (1111)x3+(0100) |
Since (1111) is the multiplicative identity, we simplify our notation as above). The solutions over ![]() to the elliptic curve equation are:
to the elliptic curve equation are:
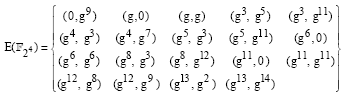 | (13) |
Since there are 19 solutions to the equation in ![]() , the group
, the group ![]() has 19+1=20 elements, i.e. the group order
has 19+1=20 elements, i.e. the group order ![]() . This group turns out to be a cyclic group of order 20. If we take P=(g3, g5) and use the addition formulae, we find group points as listed in (Table 10).
. This group turns out to be a cyclic group of order 20. If we take P=(g3, g5) and use the addition formulae, we find group points as listed in (Table 10).
Implementing an elliptic curve in ![]() with an optimal normal basis greatly speeds computation and lowers storage requirements. In addition to its speed, the elliptic curve resists breaking by current number field sieve methods and the index calculus method used by many such techniques has not been formulated for the elliptic curve. It is very likely that elliptic curve cryptography will dominate cryptosystems in the near future. Recall that in a true cryptographic application, the parameter m must be large enough to preclude the efficient generation of such a table otherwise the cryptosystem can be broken. In today’s practice, m = 163 is considered acceptable.
with an optimal normal basis greatly speeds computation and lowers storage requirements. In addition to its speed, the elliptic curve resists breaking by current number field sieve methods and the index calculus method used by many such techniques has not been formulated for the elliptic curve. It is very likely that elliptic curve cryptography will dominate cryptosystems in the near future. Recall that in a true cryptographic application, the parameter m must be large enough to preclude the efficient generation of such a table otherwise the cryptosystem can be broken. In today’s practice, m = 163 is considered acceptable.
DESIGN AND IMPLEMENTATION OF CRYPTO-SECURE COMMUNICATION PROTOCOL
Design and implementation of the right crypto-algorithm, in general, will provide the fundamental security, however, improper management of the algorithms can lead to insecure applications[1,39]. The prevention of such mishaps often lies in well-defined crypto-protocols. Perhaps the most famous in public key cryptography is the Diffie-Hellman (DH) key exchange protocol. This protocol introduced the public key concept to the world in 1976[40] and has remained a very popular protocol for strong authentication of entities. More recently, driven by needs of the embedded systems world, DH analog haven been introduced for ECC.
The Diffie-Hellman (DH) key agreement protocol is the basic public-key crypto system proposed for secret-key sharing. ECDH is the elliptic curve analog of the traditional Diffie-Hellman key agreement algorithm[40]. The Diffie-Hellman method requires no prior contact between the two parties. Each party generates a dynamic, or ephemeral, public key and private key. They exchange these public keys. Each party then combines its private key with the other party’s public key to form the shared secret. This method is also known as carrying out an ECDH key agreement[14].
The public-key crypto-schemes like RSA and ECC, when used for communication protocols for data encryption are extremely computationally demanding and thereby slower than the symmetric ones but provide arbitrary high levels of security and do not require an initial private-key exchange between two communicating parties. However, many symmetric key schemes can encrypt 1000 times faster than public key cryptosystems but are, however, poor at providing non-repudiation and key establishment functionality[39].
In real applications, however, most practical crypto-protocols are hybrid protocols, which incorporate integrated coupled symmetric and public key schemes. The public-key crypto-algorithm is first used for establishing a common symmetric-key over insecure channel[40,41]. Then the symmetric cryptosystem is used for secure communication with high throughput. Due to comparative slowness of the public-key algorithms, dedicated hardware is desirable for efficient implementation and operation of the cryptographic systems. In most applications symmetric key cryptosystems e.g., RC5, IDEA, DES/3DES and AES are today commonly integrated with existing public key cryptosystem like RSA or ECC for efficient crypto-network security.
Crypto-key length considerations: The security of the elliptic curve cryptographic schemes hinges on the apparent difficulty of the discrete logarithm problem in elliptic curve (DLP)[8]. The best algorithm known for the elliptic curve logarithm for non-supersingular curves is the Pollard-ρalgorithm[42] which takes ![]() , steps, where, r is the largest prime divisor of the order n of the elliptic curve point P. Thus, to thwart an attack, the underlying field
, steps, where, r is the largest prime divisor of the order n of the elliptic curve point P. Thus, to thwart an attack, the underlying field ![]() , the curve E and base point P should be selected so that the order n of P is divisible by a prime number r, which is sufficiently large for the purpose at hand.
, the curve E and base point P should be selected so that the order n of P is divisible by a prime number r, which is sufficiently large for the purpose at hand.
Keys in ECC are generated by relying on the Elliptic Curve Discrete Logarithm Problem (ECDLP) which is the problem of determining an integer k (provided it exists ) such that kP = Q (or equivalently, K = logPQ), where, P and Q are points on the elliptic curve[8]. ECC does not involve exponentiation, but uses multiplication, hence is not as computationally costly as RSA, which relies on exponentiation computation. Also, the underlying mathematical problem of ECC, ECDLP is fully exponential, whereas sub-exponential algorithms exist for IFP used in RSA[4]. Because it is more ’infeasible’to solve ECDLP the same level of security, can be provided with shorter keys in ECC compared with RSA.
Menezes[11] gives comparisons of the difficulty of these problems. His conclusion is that the ECDLP is computationally more difficult than the DLP or the IFP, hence, cryptosystem based on elliptic curve can be as secure as their more traditional counterparts with significantly smaller fields (Fig. 6). The expected time to solve the ECDLP with a point P as the generator having order of a 160-bit prime is approximately equal to the time required to solve the DLP with a 1024-bit modulus or to factor a 1024-bit n into primes p and q(= 2m) (Table 1).
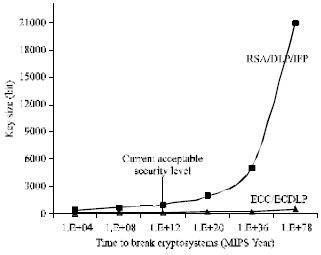 | |
| Fig. 6: | Comparison of security levels of ECC/ECDLP and RSA/DLP/IFP |
These estimates are based on the currently best-known algorithms for the problems: for the ECDLP this is Pollard’s-ρmethod; for the DLP and the IFP the best algorithm is the number field sieve. The reason for the large difference in field size for the different systems is because of the running times of the algorithms for the problems. No sub-exponential time algorithm for the ECDLP has been found that applies to general curves; the fastest for the DLP are not applicable in the elliptic curve setting. Due to these factors, ECC is better suited for low bandwidth, computational power and memory situations especially in mobile and wireless environment.
Secure key establishment and generation: Crypto-security communication network protocols usually consist of two phases. The first one is the key establishment phase, which is done initially to exchange the keys. Thereafter, in normal mode application data is transmitted over the insecure network. In key establishment phase one may use ECDH or MQV key agreement scheme. Pure DH or ECDH applications are, however, susceptible to impersonation or "man in the middle" attack, whereby an adversary establishes digital facades between two parties in order to obtain private information. Advanced key exchange protocols such as the Menezes-Qu-Vanstone (MQV) introduce mutual strong authentication which allows both parties to confidently identify each other before exchanging sensitive information[5,8,11]. It is a method of key agreement, which is related to Diffie-Hellman, but offers some significant advantages. MQV offers attributes-such as key-compromise impersonation resilience and unknown key-share resilience (the unknown key-share resilience property has been demonstrated unachievable in this version of protocol)-that are not found with ECDH. However, ECDH offers a very simple and efficient way of creating a shared secret between two entities.
Trusted third party: Certificate Authority (CA): For a added level of transaction security, a Certificate Authority (CA) can be used. A CA is a third part that is trusted to perform the service of validating information about each user and creating signed certificates to that effect. A certificate is a packet of information which includes the users (e.g. Bank’s) public key, email address, name, address and other useful information, such as expiration date of the certificate and user privileges. A CA creates, distributes, revokes and generally manages these certificates. For, example, Jane wants to obtain the Bank’s public key, she retrieves its certificate from the public key server directory and verifies the C’s signature on the certificate itself. Provided this signature verifies correctly, she has the C’s assurance that the Bank’s identity, its public key and all other information in the certificate is correct. Jane can now go ahead and use Bank’s public key to encrypt confidential information transaction to send to the Bank or to verify the Bank’s signature, protected by the assurance of the certificate.
THE ELLIPTIC CURVE DIFFIE-HELLMAN (ECDH) KEY AGREEMENT SCHEME
In Elliptic Curve Diffie-Hellman (ECDH) key exchange, the two communicating parties, sever S and client C, agree beforehand to use the same curve parameters and base point P, which generates all the points on the elliptic curve E or the order of curve #E. Each party generates their private keys kS (server) and kC (client), respectively and the corresponding public keys: QS = kSP and QC = kCP.
Both the client and server then exchange their public keys and each multiplies its private key with the other party’s public key to derive a common shared secret key: QSC = kSQC = kS(kCP) = kSCP, where, (kSC º kCS) = kMsec is the shared master private key. The shared master private key, kMsec, may now be used to encrypt or decrypt a shared message over the insecure network. An attacker cannot determine the shared private key kMsec from the curve parameters, P or the public keys of the parties.
If, however, the attacker can recover kMsec from this data then he is said to solve Diffie-Hellman Problem (DHP). However, it turns out that if the numbers are all sufficiently large , it is very hard to calculate the discrete logarithm in a reasonable time, i.e., finding. kMSec = logP QSC. The security of the Diffie-Hellman algorithm depends on this fact. It is believed for most groups in use in cryptography that DHP and the DLP are equivalent[43,44], in complexity-theoretic sense (there is a polynomial time reduction of one problem to the other and vice versa. Maurer et al.[45] has shown that breaking the Diffie-Hellman protocol was equivalent to computing discrete logarithms under certain assumptions.
Key establishment phase for wireless transaction: The client initiates a connection by relaying a ClientHello with its precomputed public key QC on the insecure wireless channel (Fig. 7).
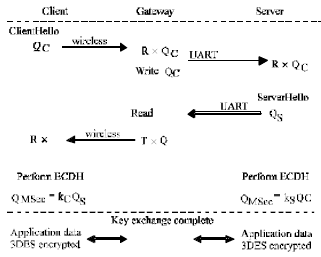 | |
| Fig. 7: | ECDH key exchange protocol |
The gate, which is in receive mode, on receiving the client public key passes it to the server through the wired interface and waits for the server’s public key. The server daemon, upon receiving the connection request sends a ServerHello with its public key QS to the gateway and then starts computing the shared master secret key from the received public key QC and the server’s secret key kS:
| (14) |
Where, QMSecret is the master secret, to be strictly kept away from the enemy. The gateway transmits the server’s public key to the client and waits for the data transmission to begin. The client, on receiving the server’s public key QS from the gateway computes the master secret:
| (15) |
The client and server now have the same shared master secret QMSecret of m-bits using the ECDH key exchange. The key for the symmetric crypto-scheme operation is then derived from this m-bit master secret.
Normal mode of operation: Once the keys are set up, the client and the sever can commence transmission of application data encrypted with symmetric-crypto scheme, e.g. Triple-DES in CBC mode[16]. To close the crypto-network connection securely, we use a close connection control message which deletes the previously generated keys.
Practical application: In a practical application, for example wireless point of sale systems, an exchange begins when a user swipes a smartcard, such as a credit, on the client device-a point of sale terminal. The client first saves the data encoded on the magnetic strip or IC device on the smartcard and then initiates the ECDH key exchange protocol.
| Table 11: | NIST Guidelines for public-key sizes with equivalent security levels[13] |
 | |
| Table 12: | Hardware implementations of ECC and RSA |
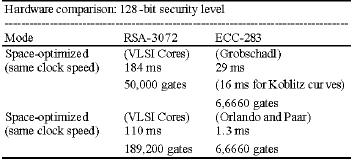 | |
After the shared master secret key is established, a symmetric crypto-algorithm like 3DES engine is fired. The card data is then encrypted with 3DES in CFB mode on the client side and the application data exchange can commence which must be securely terminated on completion of communication protocol.
Relative crypto-key sizes: So what does this mean in practice? NIST has recommended that 128-bit protection is necessary to achieve relatively lasting security (to the year 2036 and beyond) for the symmetric key crypto-schemes. This means moving from 3DES to AES[16]. To avoid compromising the security of the system, NIST's FIPS 140-2 standard[46] indicates that keys for symmetric ciphers such as AES must be matched in strength by public-key algorithms such as RSA and ECC. For example, a 128-bit AES key demands an RSA key size of 3,072-bits for equivalent security but for the same strength, the ECC key size is only 256-bits (Table 11).
ECC key sizes scale linearly, RSA does not. The result is that the gap between systems grows as the key sizes increase. This is especially relevant to implementations of AES where at 256-bit security you need an RSA key size of 15,360-bits compared to 512-bits for ECC (Table 11).
This will have a significant impact on a communication system as the relative computational performance advantage of ECC versus RSA is not indicated by the key sizes but by the cube of the key sizes. The difference becomes even more dramatic as the greater increase in RSA key sizes leads to an even greater increase in computational cost. So going from 1024-bit RSA key to 3072-bit RSA key requires about 27 times (33) as much computation while ECC would only increase the computational cost by just over 4 times (1.63).
Even in systems that use 1024-bit RSA, this has important design implications. For example, ECC-160 has a 6X smaller key-size than RSA-1024 and can generate a signature 12 times faster on StrongARM7. The performance advantage of ECC stands out even more when we look at higher security levels or when looking at hardware implementations. Table 12 makes clear the relative advantages of ECC on the hardware side of things, in terms of speed and gate count.
IMPLEMENTATION OF ELLIPTIC CURVE ENCRYPTION SCHEME (ECES) OVER FINITE FIELD GF(2m) System setup: An underlying finite field ![]() is chosen, where, q = 2m. An elliptic curve E defined over
is chosen, where, q = 2m. An elliptic curve E defined over ![]() and a point P∈E are chosen. The order of the point P is denoted by n. The field
and a point P∈E are chosen. The order of the point P is denoted by n. The field ![]() , curve E, point P and the order n, comprise the system parameters and are public-key information.
, curve E, point P and the order n, comprise the system parameters and are public-key information.
Key generation: Each communicating entity shall perform the following operations:
| • | Entity A selects a random integer kA from[1, n-1] and compute: A: = kAP. |
| • | ’s public key chain is (E, P, A) placed in public key-server, ’s private key is kA kept secrete. |
| • | Entity B selects a random integer kB from [1, n-1] and computes: B: = kBP. |
| • | B’s public key chain is (E, P, B) placed in public-key-server, B’s private key is kB kept secrete |
Encryption process (B): Entity B sends a message M to entity A and entity B performs the following steps:
| • | Look up ’s public-key: (E, P, A) or A. |
| • | Represent the message M as a pair of field elements (m1, m2), where |
| • | Accesses its private key kB. |
| • | Compute his public key point: B: = kBP: = (x1, y1) |
| • | Compute the session key: SBA: = kBA: = kB(kA)P: = kBAP: = (x2, y2), where, kBA is the shared key. |
| • | Combines the field elements m1, m2 and x2, y2 in a predetermined manner to obtain two ciphertext field elements c1 and c2. |
| • | Transmit the data C: = (B, c1, c2) to A. |
Decryption process (A): Entity A decrypts the ciphertext C: = (B, c1, c2) received from B, by performing the following steps:
| • | Look up B’s public-key: (E, P, B) or B. |
| • | Compute the session key: SAB: = kAB: = kA(kB)P: = kABP: = (x2, y2), using her private-key kA. |
| • | Recover the message m1 and m2 from c1, c2 and x2, y2. |
ELLIPTIC CURVE SIGNATURE SCHEME (ECSS)
In this age of digital piracy it is extremely important to make sure that participants of a given transaction are really who they say they are and that the communicated content is not altered in any way during the transaction. Authentication of both parties, as well as encryption of the content in transit, is critical to limit exposure on both ends of the transaction via encryption and finally signing the messages[13,39].
Digital Signatures (DS) are the electronic equivalent of handwritten signatures. A Digital Signature Algorithm (DSA) is the specific mechanism within cryptography that provide the benefits of authentication, data integrity and non-repudiation. Traditionally, handwritten signatures have provided security services because each individual has distinctive handwriting, making their signature unique and hence difficult to forge. Similarly, securing electronic information requires the equivalent of handwritten signature that cannot be duplicated. A public key construct called digital signature, a message that is unique and exclusive to the original signer, provides the solution to this problem. A digital signature’s make up is a function of both signer’s identity and the data being signed, so that any changes to the message data will effect a detectable change to the digital signature, for more detail info[39].
Two signature schemes are described in ECSS standard. In this scheme the message to be signed is first hashed to a message digest of fixed length and then this digest is signed. Verification of the signature requires both the signature and the original message[39]. Elliptic curve digital signature scheme (ECDSA) is the elliptic curve analogue of the NIST digital signature scheme (DSA)[13,47]. System Setup and Key generation as performed in a similar manner to ECES.
Signature generation for ECSS: Entity A signs a message M for entity B, by performing the following steps:
| • | Represent the message M as a binary string. |
| • | Use hash algorithm to compute the hash value e: = H(M). |
| • | Select a random number integer k where,1≤ k ≤ n-1. |
| • | Compute its public key R: = kP: = (xR, yR). |
| • | Compute r: = xR + e mod q |
| • | Use the private key kA to compute s: = k-kA r mod n |
| • | A sends to B the message M and the signature: (r, s). |
Signature verification for ECSS: Entity B verifies ’s signature (r, s) for a message M by performing the following steps:
| • | Look up ’s public-key, A. |
| • | Compute the point V = sP+rA: = (xR, yR) |
| • | Compute the hash value e: = H(M) |
| • | Compute  : = xR+e mod q. : = xR+e mod q. |
| • | Accepts ’s signature for message M if and only if r: =  . . |
Note: the hash value e reduced modulo q and then modulo n. Hence, for security reasons it is necessary that the hash function H, q and n be chosen so that, (H mod q) mod n, is also a cryptographically secure hash function. Similar operation and implementation of elliptic curve digital signature can be done using ECDSA[13] and also EC-ElGamal Signature scheme[15].
SIMPLE IMPLEMENTATION OF (ECES) OVER FINITE FIELD GF(24) System setup: The underlying finite field will be ![]() and using the generator point P = (g3, g5) which has order
and using the generator point P = (g3, g5) which has order ![]() , the data from tables 9 and 10. The system parameters (public information placed in the public-key server), are
, the data from tables 9 and 10. The system parameters (public information placed in the public-key server), are ![]() .
.
Key generation: Entity A (Alice) performs the following operations:
| • | A selects a random integer kA = 9 from[1, n-1]. |
| • | A computes the point A = kAP = 9P = (g6, 0) = ((0010), (0000)). |
| • | ’s public-key is the point A and private-key is the integer kA = 9. |
Encryption process (B): (Entity B sends a message M=10101011 to entity A). Entity B performs the following steps:
| • | Looks up ’s public-key from public-key server: A = (g6,0). |
| • | Represents M as a pair of field elements M = (m1, m2) = ((1010), (1011)) = (g5, g14) |
| • | Selects a random integer kB = 14 from[1,19] |
| • | Computes his public key: B = kBP = 14P = (g8, g13) = ((1001), (1101)). |
| • | Compute shared key: SBA: = kBA = kB(kAP) = 14(9)P = 6P = (x2, y2) = (g8, g3) = ((1001), (0100)). |
| • | Compute the field element: |
| • | Now B forms x4 = (1000) = g9 by concatenating the high order 2-bits of |
| • | B forms the field elements: |
| (16) |
| (17) |
| • | B transmits the data the ciphertext C: = (B, c1, c2) parameters to A, i.e.,: |
| C: = (g6, 0, g13, g8) = ((0010), (0000), (1101), (1001)) |
Decryption process (A): Entity A decrypts the ciphertext, C: = (g6, 0, g13, g8), received from B, by performing the following steps:
| • | A computes the session key: SAB: = kAB = 14(9P) = 6P = ( g8, g3) = ((1001), (0100)).. |
| • | A forms x4 = (1000) = g9 and y4 = (1001) = g8 just as B did. |
| • | A recovers the pair (m1+x2,m2+y2) by computing: |
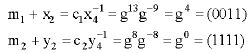 |
| • | A recovers the message pair: m1 = (0011) + g8 = 1010 and m2 = (1111) + g3 = 1011, which is the original message: M = (m1, m2) = (g5, g14) |
Simple implementation of EC Signature Scheme (ECSS) Signature generation scheme: Entity A signs the message M = 777 = 1100001001. Suppose that the hash value of ![]() A performs the following steps:
A performs the following steps:
| • | Select a random integer k = 13 in the range[1,n -1]. |
| • | Compute R = 13P = (g11, g11) = (xR, yR) |
| • | Represent xR = g11 = (1110) as the integer: xR = 8 + 4 + 2 = 14 |
| • | Compute |
| • | Use its private key kA=9 to compute: S = k-kAr(mod n) = 13 = 9(7) mod 20 = 10 |
| • | The signature on message M is: (r, s) = (7, 10). |
Signature verification for ECSS: Entity B verifies signature (r, s) = (7, 10) on M as follows:
| • | B looks up ’s public-key: A = (g6, 0) = 9P. |
| • | B computes the point: V = sP + rA = 10P + 7(9P) = 13P = (g11, g11) = (xV, yV) |
| • | Represent xV = g11 = (1110) as the integer: xR = 8 + 4 + 2 = 14 |
| • | B computes |
| • | B accepts ’s signature on M since |
THE PRACTICAL APPLICATION OF ECC
Implementing ElGamal ECC over finite field GF(2163): Crypto-scientist T. ElGamal was the first mathematician to propose a public-key cryptosystem based on the Discrete Logarithm Problem (DLP) modulo prime p[48]. He in fact proposed two distinct cryptosystems: one for encryption and the other for digital signature scheme in 1984, well before elliptic curves were introduced in cryptography. Since then, many variations have been made on the digital signature system to offer improved efficiency over the original system. In 1991, Claus Schnorr discovered a variant of the ElGamal digital signature scheme, which offers better efficiency, compared to the original systems. In turn, the U.S. government’s Digital Signature Algorithm (DSA) is based on ElGamal’s work[39] The ElGamal public-key encryption scheme can be viewed as Diffie-Hellman key agreement protocol in key transfer mode[49]. Its security is based on the intractability of the Discrete Logarithm Problem (DLP) and the Diffie-Hellman problem. These systems are the best known of a large number of systems whose security is based on the DLP. The prime p used in the DL systems should also be at least 150 decimal digits (500 bits) in lengthto provide short-term security. The elliptic curve cryptosystems as applied to ElGamal protocols were first proposed in 1985[49].
In implementing ElGamal elliptic curve cryptosystems, suppose that two entities, the eBusiness (B) and the customer Alice (A) wants to communicate between each other over an insecure communication network. Next let’s assume that the two entities have decided to use the protocol of EC-ElGamal encryption protocol to implement their secure communication. One basic point to note is unlike ECDH protocol[8,14], this protocol does not create a common key, but using EC-ElGamal protocol a message M = M1+M2, not necessarily a point on elliptic curve, can be sent from eBusiness to Alice and vice versa.
Let the fixed point P = (xP, yP) ∈ GF(2m) be the generator point such that the multiples kP of the generator point P are (for 1 ≤ k ≤ n-1) including point O located at infinity. Now suppose entity A chooses public-key set: A = kAP, where the secret-key kA is selected from [1, n-1], giving rise to its public-key ring (E, P, A), which is kept in the public-key server. Next entity B selects a random secret-key kB from [1, n-1] such that: B = kBP giving rise to its public-key ring (E, P, B) kept in the public-key server.
The sender A encrypts her message M = M1 + M2 by making use of the key exchange protocol e.g. ECDH key agreement scheme to generate a shared key: SAB = kA(kBP) = kABP = kBAP = (xS, yS). She then performs the message encryptions as follows: C = (c1, c2) = MSAB, preferably, c1 = M1xS and c2=M2xS, where M = M1+M2. The encrypted ciphertext message is then sent as a package: (A, C).
Once the encrypted ciphertext is received by entity B, it looks up ’s public-key from the public-key server and computes: SBA = kB(kAP) = kBAP = (xS, yS). Subsequently ![]() and
and ![]() and the original plaintext message is M = M1+M2 is recovered. It should be noted that for the message communication between the parties to take place each must exchange their public key for the purpose of key agreement computation. Secondly, in obtaining the original message, two inversion multiplications are performed. Note that in setting up the parties public keys, we can also compute hkAP and hkBP, which can resist the attack on small subgroup. Where, h is a co-factor defined in P1363[19].
and the original plaintext message is M = M1+M2 is recovered. It should be noted that for the message communication between the parties to take place each must exchange their public key for the purpose of key agreement computation. Secondly, in obtaining the original message, two inversion multiplications are performed. Note that in setting up the parties public keys, we can also compute hkAP and hkBP, which can resist the attack on small subgroup. Where, h is a co-factor defined in P1363[19].
Hardware design and implementation for ECC: The current state of global communication coupled with global economy requiring the global prime movers to be in contact at all times with the business point is driving the world of wireless communication powered by embedded constrained environment devices technology to a new high.
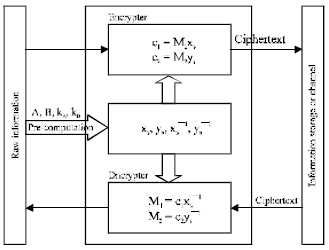 | |
| Fig. 8: | Encryption and decryption schemes when the encrypter and decrypter are sitting aside |
But the world of embedded constrained systems with its limited power, memories and storage capabilities is limiting effective implementation of better crypto-algorithms. However, with the advent of ECC coupled with AES-a symmetric key crypto, the world of embedded constrained devices is beginning to enjoy better crypto-security network connections, thereby allowing secure business transactions over-the-air on the fly.
The elliptic curve crypto-schemes offer the highest security per bit ratio compared to any other currently known public-key cryptosystems. This is a plus point for embedded systems where the cost increases significantly with every extra memory chip. ECC hardware implementation uses fewer transistors, e.g., currently implementation of 155-bit ECC uses only 11,000 transistors compared to RSA 512-bits implementation with 50,000 transistors.
The elliptic curve crypto-schemes with key size in the range of 155-210 bits is currently considered acceptable for practical crypto-security protocols which compares favorably with similar security level as the Discrete Logarithm Problem (DLP) and IFP crypto-schemes with the key size of 512-1024 bits. Thus, ECC is superior to DLP/IFP cryptosystems in terms of block length and storage requirements. Our practical implementation is based on the key size of 163-bits where GF(2163). The procedure required for successful implementation of hardware based protocols is as follows:
| • | To minimize the hardware complexity (circuitry complexity, feedback loops and the number of XOR-gates), the irreducible polynomial, f(x) = x163 + x7 + x6 + x3 + 1, was chosen. |
| • | The integers a, b ∈ GF(2163) required for the obtaining the elliptic curve, E: y2+xy = x3+ax2+b were chosen arbitrarily as: |
| a =4 | FEEE CE35 5F00 D401 875F E2C0 FFF3 EE2F 64FC B30D |
| b =1 | 31C8 335B 7F5A D1C5 EEA0 8316 0E10 C9C8 C3B3 D39A |
| • | With a and b chosen as above, there could be a possible solution to the elliptic curve E, which yields an arbitrary fixed point P = (xP, yP) on the curve: |
| xP = | 5 5968 5D73 DD75 4D33 7FF7 3319 706C FF36 8212 25AF |
| yP = | 3 6F4D 089A 3FA0 C2CB F84E 0D6E FCB4 1033 362A 5B97 |
Which we use as the generator of the point of order #E the number of points on the curve.
| • | At this point and regardless of the computing complexity at this step, sender chooses her private kA and looks up at the receivers public-key B = kBP with kB being its private key which are given by: |
| kA = 95 and kB = 250 both from [1, n-1], respectively. |
| • | The encrypter entity A computes, SAB = kA(kBP) = kABP = (xS, yS), where: |
| xS = | 4 A0AF DCE6 AFB4 2309 D155 BFBA 9D49 6178 07B5 885D. |
| yS = | 459E 2437 4FB9 1C44 D5F4 42E3 57E2 BB32 F6B6 91C9 |
| • | The ciphertext messages are then computed as: c1 = M1xS and c2 = M2xS where M1 and M2 are consecutive blocks of which the data length is m-bits (163 bits), in this case we have a single block: |
| M = | M1 + M2 = 33E1 3366 8832 5566 5CCA + 3FE1 3CE6 8832 5577 5CEA |
| c1 = | M1xS =1EF DB1F 61D8 AF59 AD11 F520 723C F6C2 AC96 364C |
| c2 = | M2xS =5 AD61 C6F5 869E BAC1 AB1E F1F1 C272 8FD4 6567 380E |
| • | The encrypted messages are next feed and stored in the array of Flash ROMs, which can be part of an Integrated Chip (IC) module or can be on a separate module. |
The last two operations can be repeated many times until all the data messages are encrypted and stored (or sent). To recover the encrypted messages, the receiver performs the following operations:
| • | The shared key agreement SBA = kB(kAP) = kBAP = (xS, yS) is already pre-computed as above. |
| • | Step (1) and (2) could be omitted since the encrypter and decrypter are in the same module. From above (xP)ˉ1 and (yP)ˉ1 can be computed as: |
| (xP)ˉ1 = 5 6468 AAC3 D57A 35E0 E19F BF40 5F1B 18F1 C861 6C5E (yP)ˉ1 = 7 223D BA66 4DAA 8495 603B C053 B084 2A3A 82C0 5CAE |
| • | Subsequently: |
M1 = c1(xS)ˉ1 = 33E1 3366 8832 5566 5CCA M2 = c2(yS)ˉ1 = 3FE1 3CE6 8832 5577 5CEA |
The last operation is to be repeated until all the plaintext is recovered from the transmitted ciphertext messages in case of large volume message.
The hardware design considerations: The elliptic curve ElGamal cryptosystems discussed above can be implemented in hardware using a simplified circuit in which the encrypter and the decrypter circuit modules are integrated aside within the same IC hardware. Therefore, xS, yS, (xS)ˉ1 and (yS)ˉ1 can be pre-computed in advance and stored in the registers. The encrypter task is then just to compute:
| c1 = M1xS and c2 = M2yS |
At the receiving end, the decrypter has then to compute:
| c1(xS)ˉ1 = M1xS(xS)ˉ1 = M1 and c2(yS)ˉ1 = M2yS(yS)ˉ1 = M2 |
To recover the original plaintext. The complete operation is illustrated in the schematic hardware design concept shown in Fig. 8.
The advantage of this coupled encrypter-decrypter architecture approach is that only minimum hardware is required, such that a single fix-coefficient multiplier can be used to perform encryption or decryption depending on the mode of operation the chip is programmed to undertake. The multiplier can also be used in half duplex mode to perform an alternate encryption or decryption. Note that multiplication is performed over Galois field, therefore, the selection of the irreducible polynomial can affect the circuitry complexity. In practice, select the one that has small number of terms (pentanomial, or 5-terms). The IC module capability can be improved using additional circuitry capable of solving elliptic curve equations, inversion and multiplication, thereby enabling it to generate/change the private and/or public keys on-the-fly (Fig. 3 and 4). This additional circuitry no longer allows for a simple circuit and has added complexity which requires VLSI technology which by today’s standard is not difficulty to achieve. Hardware based elliptic curve cryptosystems have already been implemented under various constrains and applications. Sutiko et al.[50] have implemented the ElGamal ECC processor in 32 bit-wide bus with 155 bit-wide register. Paar[51] looked at the implementation of the multiplier which is applicable to a composite field.
In this study we have shown how to implement elliptic curve cryptosystems over binary finite field, ![]() using polynomial basis representation and; normal and optimal normal basis representations. We have shown that the elliptic curve crypto-schemes offer the highest security per bit ratio compared to any other currently known public-key cryptosystems. This is a plus point for embedded systems where the cost increases significantly with every extra memory chip. ECC hardware implementation uses fewer transistors, e.g., currently implementation of 155-bit ECC uses only 11,000 transistors compared to RSA 512-bits implementation with 50,000 transistors. Elliptic curve crypto-schemes offer a lot of promise in terms of security and memory requirement than any other present crypto-schemes. However, more research is needed in this field for better understanding and effective implementation of ECC.
using polynomial basis representation and; normal and optimal normal basis representations. We have shown that the elliptic curve crypto-schemes offer the highest security per bit ratio compared to any other currently known public-key cryptosystems. This is a plus point for embedded systems where the cost increases significantly with every extra memory chip. ECC hardware implementation uses fewer transistors, e.g., currently implementation of 155-bit ECC uses only 11,000 transistors compared to RSA 512-bits implementation with 50,000 transistors. Elliptic curve crypto-schemes offer a lot of promise in terms of security and memory requirement than any other present crypto-schemes. However, more research is needed in this field for better understanding and effective implementation of ECC.