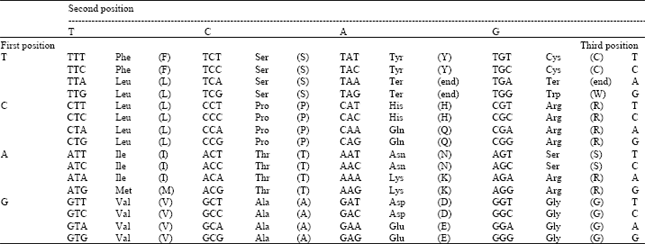
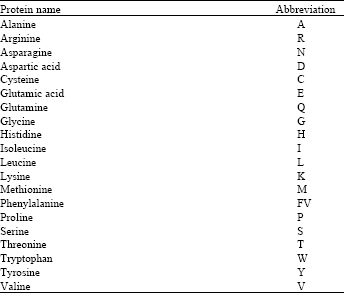
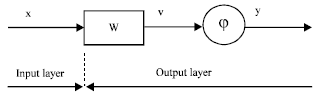
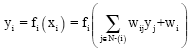Research Article
Predicting Protein Secondary Structure Using Artificial Neural Networks: Current Status and Future Directions
Faculty of Applied Sciences, Sohar University, Sohar, Sultanate of Oman
Safaai Deris
Faculty of Computer Science and Information Systems, University of Technology Malaysia, UTM Skudai, Johor, Malaysia