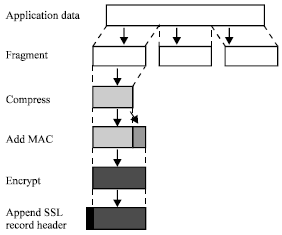
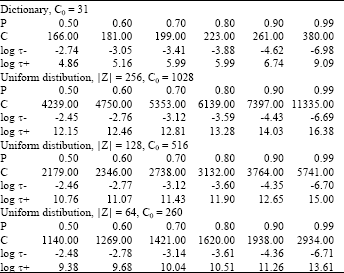
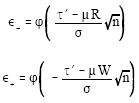Research Article
Password Interception in a SSL/TLS Channel
Department of Computer Science, International Islamic University Islamabad, Pakistan
Umar Waqar Anis
Department of Computer Science, International Islamic University Islamabad, Pakistan
Tauseef ur Rahman
Department of Telecom and Computer Engineering, International Islamic University Islamabad, Pakistan