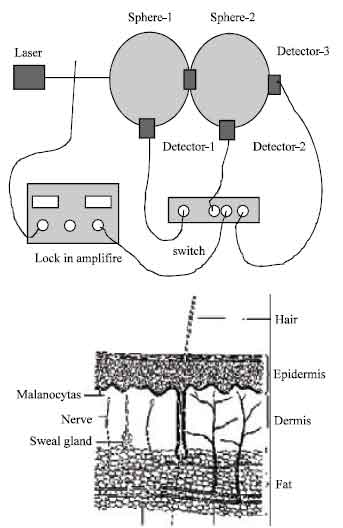
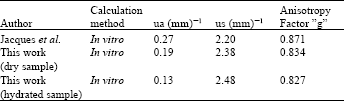
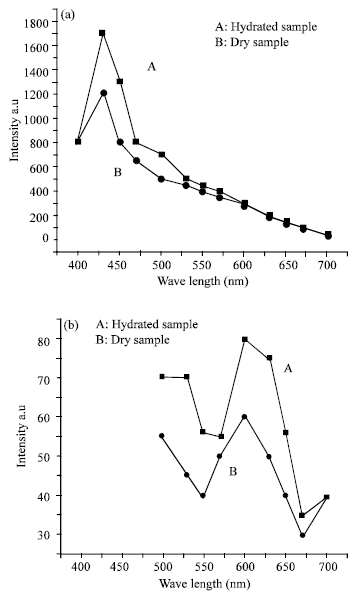
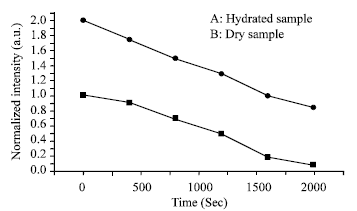
Research Article
Measurement of an Optical Parameters: Absorption Scattering and Auto-florescence of Skin in vitro
Laser Laboratory, Department of Physics and Applied Mathematics, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, Pakistan
M. Ikram
Laser Laboratory, Department of Physics and Applied Mathematics, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, Pakistan
M. Nawaz
Applied Physics Division, Pinstech, Post office Nilore, Islamabad, Pakistan
M. Aslam
Applied Physics Division, Pinstech, Post office Nilore, Islamabad, Pakistan