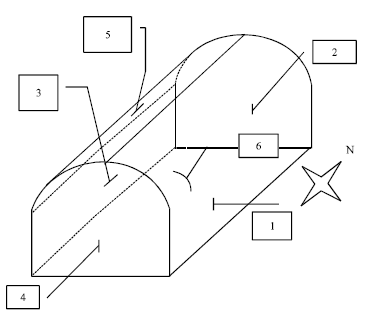
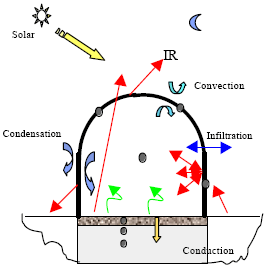
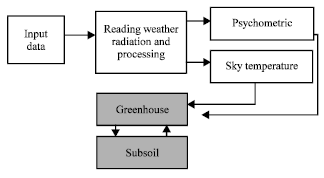
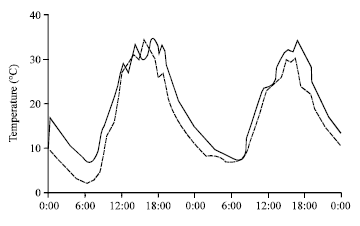
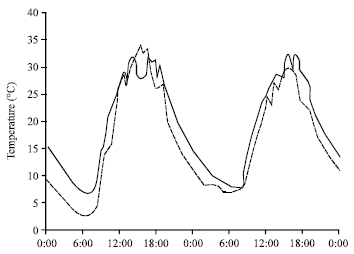
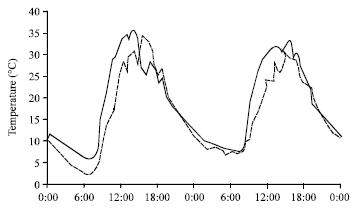
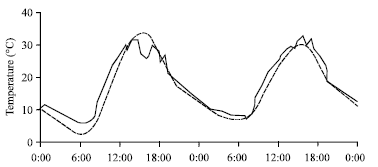
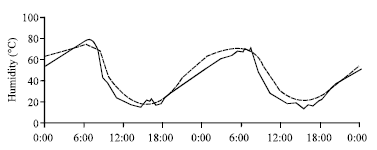
Research Article
Numerical Analysis of the Influence of Soil-Air Convective Heat Transfer Coefficient on the Global Indoor Climate Model of a Closed Plastic Tunnel Greenhouse
Applied Research Unit on Renewable Energies, Ghardaia, Algeria
H. Benmoussa
Applied Research Unit on Renewable Energies, Ghardaia, Algeria
P.E. Bournet
Environmental Physics and Horticulture Research Unit, Agrocampus-Ouest, Angers, France