Wavelet Estimation of Systematic Risk at Different Time Scales Application to French Stock Market

INTRODUCTION

In this study, we continue a study that has started in Rhaeim et al. (2007) about the estimation of systematic risk in CAPM. Such a subject is one of the most commonly used models in asset pricing theory and practice. Sharpe (1964) and Lintner (1965) flowing the suggestions of mean variance optimisation in Markowitz (1952) originally propose it and it has provided a simple and compelling theory of asset market pricing for more than 20 years. Several authors have contributed to development of a model describing the pricing of capital assets under conditions of markets equilibrium. The analysis of the theoretical empirical model is presented by several studies. In Campbell (2000), it has proved that the relationship founded by the CAPM was roughly linear, although the slope was too flat to support the CAPM strongly.

Later studies focused on the impact of return interval of betas. This research point out the importance of time scale issue. In Fama (1980, 1981), it has shown that the power of macroeconomic variables in explaining the stock prices increased with increasing time length. Kothari and Shanken (1998) concluded that Fama and French’s results hinge on using monthly rather than yearly returns. Than Handa et al. (1989) provided evidence that different beta estimates were possible for the same stock, if different return intervals were considered.

The principal idea of Rhaeim et al. (2007) was the use of quite random scale periods for estimating the CAPM. A dyadic scale sequence of periods has been used firstly. Next, a triadic one has been acted in order to control the possible effects of the scaling behaviour of the risk. Our idea has been proved to be robust and so it has yielded interesting results among the well known ones. However, some incoherence has appeared for large scales. This fact lets us to think about adaptable methods in order to understand or to resolve the ambiguity.

In this study, present object is to investigate the beta behaviour (systematic risk) at different time horizons. A wavelet-based method is analysed to estimate the capital asset pricing model at different time scale. The idea is as usual the use of semi-random scale periods. Recall that wavelets are strongly related to scaling procedures while an analysing basis is always obtained from a source function called mother wavelets by scaling actions and translations. This strong relation has affectively enabled us to obtain good results. The resulting method is tested for empirical results to control the relationship between the return of a stock and its beta. This relationship often becomes stronger as the scale increase. Therefore, the predictions of the CAPM are more relevant in a multi scale framework as compared to short time horizons.

Backgrounds on Wavelet Analysis
Wavelets are mathematical tools that are widely applied for analysing time series. The starting point in such an analysis is based on decomposing a time series on scale-by-scale basis in order to control the series structure at different time horizons. Wavelets basis are obtained from some source functions (φ, Ψ) called (father,mother) wavelet by dilations and translations (Gencay et al. (2002). Usually the wavelet basis elements are defined by;

(1)

One usually associates some coefficients

(2)

The S_{j, k} are known as the smoothness coefficients or approximation coefficients and the d_{j, k} the detail coefficients or wavelet ones. The wavelet series of f at the level J is:

(3)

This series represents the decomposition of the signal into orthogonal signal components at different scales. More specifically, the detail coefficients d_j,k,…, d_1,k capture the higher frequency oscillations and so they represent fine scale deviations of the trend. The S_j,k’s represent the smooth coefficients that capture the trend. So that, the wavelets series approximation of the original signal f is composed of a superposition of smooth part signal and detail signal parts as follows:

(4)

Where:

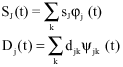Wavelet Estimation of the CAPM
The capital asset pricing model implies that the excess return from asset i should be proportional to the market premium. The derivation of the CAPM equation is based on the assumptions of risk-averse investors, frictionless markets, absence of information costs and information asymmetries, unlimited borrowing and fending at the risk-free rate and perfect divisibility and marketability of financial assets (Copeland et al., 2004). The CAPM established that the expected return is governed by the equation:

(5)

Where, R_j is the return on asset i, r_f is the risk-free rate, R_m is the return on the market portfolio and

(6)

The market risk premium is assumed by the return (E (R_m –r_f). It represents the return over the risk-free rate required by investors to hold the market portfolio. Equation 5 can be re-written to express that the risk premium on individual asset is obtained from its beta and the market risk premium. We have precisely

(7)

In empirical finance, the usual estimator for β_i is the OLS estimate from the following regression

(8)

Where, ε_it is a white noise.

Wavelet variance analysis consists in decomposing the variance of time series into sequences associated to different time scales. The basic idea is to substitute the notion of variability over some scales to globally measure the variability estimated by the sample variance. If we assume that the dependence structure of the market returns (r_mt) is independent of time, an unbiased estimator of wavelet variance will be then;

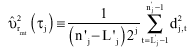(9)

Where:

d_j,t = The wavelet coefficients of variables at scale

τ_j. n_j = n/2 = The number of such coefficients

n = The sample size

L_j = (2^j – 1) (L–1)+1 = The length of the scale wavelet filter Fermandez (2006)

Similarly, the wavelet covariance can also decompose the sample covariance into different time scales. It indicates the contribution to the covariance between two stochastic variables. The unbiased wavelet covariance between market return r_mt and the stock return r_it at scale τ_j can be expressed as follow (Fermandez, 2006).

The wavelet beta estimator for asset i at scale j is defined by

Data and Empirical Results
Present data set is extracted from the web-basis http://finance.yahoo.com and it consist of some stocks in the CAC 40 index between January 1, 2002 and December 30, 2005. The CAC 40 index is taken to be the corresponding market portfolio. The risk free rate of return is assumed to be the daily Euro Interbank Offered Rate (EURIBOR) at which euro interbank term deposits within the euro zone are offered by one prime bank to another. Stocks prices are adjusted for dividends and splits. It gathers the forty stocks that most actively traded over the past years. The sample size is 1044 market days or roughly 4 years.

We estimate the CAPM at different time scales for this group of stocks regularly traded on the French market. Rhaeim et al. (2007)’s data is applied inn the study and summary descriptive stat (mean, standard deviation of the statistical variables). Our object is to study the relationship between excess return on each individual stock and its beta. In particular, during the entire sample period, the beta of each individual stock is computed using the wavelet beta estimator based on the Haar wavelet filter of length L = 8 for scales j = 1, 2....,6. The daily return of each stock is the log price difference

Where, P_it is the price of asset i at day t. The market return R_mt is taken as the log difference of the CAC 40 index:

Where, C_t is the index value at day t.

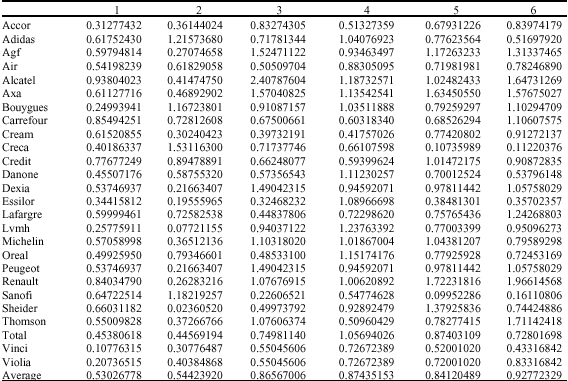
Table 1:	Beta for each scales

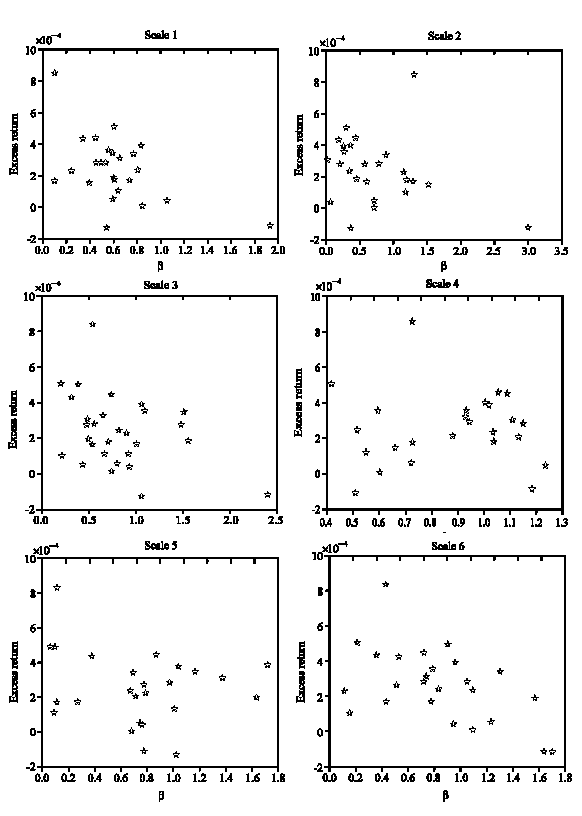Fig. 1:	The average excess return on each individual stock (vertical axis) versus corresponding beta at different scales

The beta of each individual stock is evaluated from Eq. 11 for scales j = 1, 2,…, 6. Since we employ daily data in our analysis, wavelet scales are such that scale 1 corresponds to the period of 2-4 days, scale 2 to 4-8 day dynamics, scale 3 to 8-16 day dynamics, scale 4 to 16-32 day dynamics, scale 5 to 32-64 day dynamics, scale 6 to 64-128 day dynamics.

Table 2:	The OLS of average excess return/average stock beta at different scales
The slope and the constant are multiplied by 100 for reporting purposes. One star (*) indicates that the coefficient is significant at the 10% level of significance and three stars (***) at 1%

Scale 6 is the highest one at which we can evaluate the beta of each stock because the following one correspond to 128-256 day dynamics, i.e., approximately one year. Table 1 reports our estimation results.

When looking at individual systematic risk, the beta of the stock tends to increase as the scale increase. In particular, the relationship between excess return and the market portfolio becomes stronger at the higher scales. Therefore, the estimated beta differed considerably depending on the scale of estimation. Figure 1 shows that return and beta are near linear form for 1, 2 and 6 scales. Gencay et al. (2005) states that for USA, UK and Germany beta and return are stronger form as scale increases. We found that return and beta are stronger form at 1, 2 and 6 scales but not 3, 4, 5 scales and this shows that French stock market differs from USA, UK and Germany.

In order to study the robustness of the relationship between the return of the stock and its beta, we estimate the slope between the two variables. Table 2 reports the OLS estimate of the regression coefficient of each average stock excess return (dependant variable) against the average beta of stock (independent variable) at different time scales. OLS of average excess return/average stock beta shows that the relationship between return and beta are stronger at 1 and 6th scale and this shows that French market is efficient at shorten (2-4 days) and longer period (64-128 days). These facts enforce our earlier conclusion that the fourth scale (capturing dynamics with a period of 16-32 days) explains the excess return-beta relationship much better than other scales during the sample period. Therefore, the CAPM is a multi scale phenomenon, shorter and longer time scales are more relevant in explaining the relationship between the stock return and its beta. Viviana (2005) draws nearly similar conclusions for a sample of 24 stocks traded on the Santiago Stock Exchange.