Research Article
Investigation of the Thermal Properties and Anti-microbial Behavior of Socks Knitted from Conductive Yarns
Department of Spinning, Weaving and Knitting, Faculty of Applied Arts, Helwan University, Giza, Egypt
A sock is an item of clothing worn on the feet. The foot is among the heaviest producers of sweat in the body, as it is able to produce over 1 US pint (0.471) of perspiration per day. Socks help to absorb this sweat and draw it to areas where air can evaporate the perspiration. In cold environments, socks decrease the risk of frostbite. The earliest known surviving pair of socks, dating from 300-500AD these were on the Nile in Egypt. In the twelve century cotton sock, found in Egypt. The invention of a knitting machine in 1589 meant that socks, could be knitted six times faster than by hand. Nonetheless, knitting machines and hand knitters worked side by side until 1800 (Smith and Pitts, 2009). The next revolution in sock production was the introduction of nylon in 1938. Until then socks were commonly made from silk, cotton and wool. Nylon was the start of blending two or more yarns in the production of socks, a process that still continues.
Socks can be created from a wide variety of materials. Some of these materials are cotton, wool, nylon, acrylic, polyester, olefins, (such as polypropylene), or spandex. To get an increased level of softness other materials that might be used during the process can be silk, bamboo, linen, cashmere, or mohair (Anonymous, 1996). Socks should be designed in the way to meet the customer pleasure in accordance with fashion and needs, have high use performance without losing post-production properties and their fiber properties which used especially for health shouldn’t affect negatively human health. (Tatsuya, 2001).
The quality in socks can vary depending on many factors. These can be summarized as; the type and properties of the used thread, knitting conditions and machine properties, finishing method and the used finishing materials and the form giving operation applied on socks (Onder and Candan, 2005).
In addition to this, basic properties expected from socks during usage are resistance against abrasion, elasticity, constant post-washing dimensions, thermo-physiological properties and physiological comfort. Providing optimum heat, damp and air passing are expected from socks through physiological comfort. And with thermo-physiological comfort, perceiving the fabric comfort on the skin and feelings providing sensations of warm, cold, wet and touch positively are understood (Ozdil, 2008).
Knitted fabrics not only posses stretch and provide freedom of movement but they also have good handle and comfort. That is why knitted fabrics are commonly preferred for sportswear, casual ear, underwear and socks. The comfort provided by clothing depends on several factors, one of them being thermal comfort. It is known that fiber type, yarn properties, fabric structure, finishing treatments and clothing conditions are the main factors affecting thermo-physiological comfort (Li, 2001). A state of comfort can only be achieved when the most complex interactions between a range of physiological, psychological and physical factors have taken place in a satisfactory manner. Hence, the comfort provided by clothing depends on such factors as softness, flexibility, moisture, diffusion, air permeability, thermal comfort, etc. (Marmarali et al., 2009).
Human thermal comfort depends on a combination of clothing, climate and physical activity. The warmth of a fabric is due to insulation provided by air trapped between fibers and yarns. Fabrics from straight filament yarns remove heat rapidly by conduction when placed next to the skin and in such a way produce a so-called cool feel or handle. This phenomenon occurs just for a moment because the skin adapts rapidly to mild stimulations. Fabrics from hairy yarns feel warm on contact with the skin due to the insulating air held between the fabric fibers and the skin (Ogulata 2007).
With the aim of making comfortable socks, we not only used cotton yarns but also a new industrial method of making yarns of conductive fibers with traditional fibers such as cotton or polyester. These fibers have a good influence on humans because they are naturally antibacterial and biodegradable, have a high moisture absorption capacity, softness, brightness UV protective properties, good mechanical and physical performances and antiphlogistic, antiallergic properties (Ucar and Yýlmaz, 2004).
Wearing safety footwear without suitable antibacterial socks, can lead to severe foot irritation and discomfort. The main purpose of anti-bacterial socks is to eliminate bacteria which multiply in the presence of dirt, moisture and heat which cause infections of the foot body odor and allergies. The average person loses upto 250 mL of water a day from their feet in the form of perspiration. Anti-bacterial socks being largely constructed of cotton which is hydrophilic and will conduct moisture away from the body (Gomathi, 2009).
The effectiveness of anti-static footwear is compromised if the hosiery socks do not also conform to acceptable anti-static requirements. For this purpose we use anti-static, an innovative fiber that has a layer of copper bonded to it. Anti-Static fiber is strategically placed in order to conduct static electricity away from the body, through the sock to the shoe (Baumgartner, 2000).
Copper is an essential nutrient in the human body. It also effectively kills many species of bacteria, fungus and viruses. It has been used for health, wellness and antimicrobial purposes for thousands of years, dating back to the ancient Egyptians. Copper plays an important role in the healthy function of many systems and organs within the body, including the nervous and immune systems and the heart, brain and skin. In the medical arena, researchers have also documented copper’s value in stimulating the production of hemoglobin (red blood cells), collagen and other key proteins that help stabilize skin layers, promote wound healing. In cosmetic applications copper improves the look and appearance of skin and get rid of smelly feet. This patented non-toxic, antimicrobial and antifungal technology helps eliminate fungi, bacteria causing odor on the sock as well as improving the regeneration and appearance of the skin (http://www.Antimicrobialcopper.com).
The objects of this investigation is to determine the functional properties including thermal properties and anti-microbial behavior of socks manufactured using not only traditional cotton or polyester yarns but also yarns of new kinds of conductive fibers such as copper fibers. The functional properties influenced by both material type and knitted structure parameters. The effect of socks constructions parameters on their functional properties for plain and rib knits was discussed.
The weft knitted samples were produced on circular hosiery weft knitting machine as the yarns are running continuously around the fabric. Five samples were produced using plain (s. Jersey) structure; another five samples were produced using Rib (1x1) structure. The raw materials used are traditional yarns (cotton or polyester) or mixed yarns (cotton, polyester and conductive yarns) which should be taken to reduce or eliminate the buildup of electrical charges and enhance the thermal conductivity and anti-microbial behavior of produced socks. These "conductive" yarns are knitted with the base yarns in a different percentage to obtain the required functional properties.
Fibrous base material: Variation in fiber properties can lead to significant variation in the finished product. The fiber type, denier, length, cross-sectional shape, surface texture and finish all influence the quality of the final end-use product. The type of conductive fibers which is used to produce the samples are composed of polyamide 66 with a layer 0.2 μm thick of conductive copper sulphide fused by chemical process into the outer skin of the fiber which has a reddish brown color in its final form. The layer of copper sulphide is intimately integrated into the polymer ensuring a permanent resistance to the usual wear conditions and various chemical treatments. They can be used to bring into focus the following:
| • | Excellent conductivity level: 105 ohm cm-1 |
| • | Excellent textile characteristics |
| • | Excellent antibacterial properties |
Table 1 shows the properties of copper sulphide grafted onto nylon fibers which were used to produce the samples.
Yarns specifications: There is a relationship between the origin and structure of the yarns used to make a fabric and its physical and functional properties. The method of construction can also affect the fabric behavior. To produce the weft knitted samples, different types of the yarns were used. The basic yarns (type) are cotton or polyester used alone or mixed with conductive yarns in a different percentage according to the construction of the textile material, the conditions of process, the use and the functional properties obtained.
| Table 1: | Properties of copper sulphide grafted onto nylon fibers |
| Table 2: | Specifications of utilized yarns |
 | |
| Table 3: | Specifications of the socks samples |
 | |
| Conductive material: Copper sulphide grafted onto nylon | |
The specifications of these utilized yarns are summarized in Table 2.
Manufacturing methods: It is important to know the fabrics constructions and their properties to choose them for the purpose which they are most suitable. All samples were produced on circular hosiery weft knitting machine (Diameter 3", Gauge 12 with 6 Feeders).
The specifications of the samples which were produced could be seen in Table 3. The difference between the samples depends on the various yarn constructions, the ratio of conductive material and the structure.
Measurements of manufactured samples: Several tests were carried out in order to evaluate the functional properties of produces socks, these tests include mechanical and physical properties tests:
| • | Thickness test: The thickness samples were measured by the Teclock tester under a pressure 0.2 kg f cm-2 according to the ASTM D1777-96 (2011) e1 |
| • | Weight test: This test was carried out by using Mettler H 30 apparatus according to the ASTM ASTM D3776/D3776M-09(2009) |
| • | Bursting strength test: This test was carried out for all samples by using the strip method according to the ASTM D3786/D3786M-13 (1996) |
| • | Air permeability test: This test was carried out for all samples, according to the ASTM D737-04 (2012) |
| • | Water resistance test: This test was carried out for all samples, according to the ASTM D570-98 (2010) |
| • | Thermal resistance test: This test was carried out for all samples, according to the ASTM D1518-11a (1996) |
| • | Fabric weariness or abrasion tester: This test was carried out for all samples, according to the ASTM D3885 (2007) |
| • | Determination the growth rate of bacteria (E. coli and S. aureus) and fungi (T. viridae and A. niger) test: This test was carried out for all samples, according to the AATCC Test Method 30 (2013) |
Since, the main aim of this work is to design comfortable healthy socks with better functional properties, different fabric types with various constructions parameters were made. Test results were addressed and discussed in order to optimize the socks design parameters.
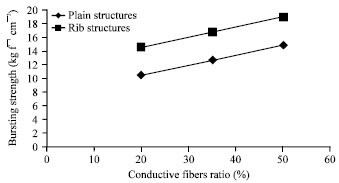
Bursting strength: Figure 1 shows the effect of conductive fibers ratio (%) on bursting strength values (kg f cm-2) for experimental samples No. (2, 3, 5, 7, 8 and 10).
It is observed that, as shown in Fig. 1, there is a direct relation between the conductive fibers ratio (%) in the fabric and its bursting strength values. As the conductive fibers ratio (%) increases, the bursting strength values increase in produced samples.
 | |
| Fig. 1: | Effect of conductive fibers ratio (%) on bursting strength values (kg f cm-2) for experimental samples |
To get a mathematical relationship between the conductive fibers ratio (%) in the plain knitted samples on the bursting strength values (kg f cm-2), a linear regression technique was used to get this relationship. The following equation is applied on the (kg f cm-2) values:
| (1) |
| Y | = | Bursting strength values (kg f cm-2) |
| X | = | Conductive fibers ratio (%) |
As R = 1, the correlation is considered too high which means that the regression equation is reliable for prediction of the bursting strength values (kg f cm-2) in the conductive fibers ratio (%) range using plain knitted structure.
To address a mathematical relationship between the conductive fibers ratio (%) in the rib knitted samples on the bursting strength values (kg f cm-2), a linear regression technique was used to get this relationship. The following equation is applied on the (kg f cm-2) values:
| (2) |
| Y | = | Bursting strength values (kg f cm-2) |
| X | = | Conductive fibers ratio (%) |
As R = 1, the correlation is considered too high which means that the regression equation is reliable for prediction of the bursting strength values (kg f cm-2) in the conductive fibers ratio (%) range using Rib knitted structure.
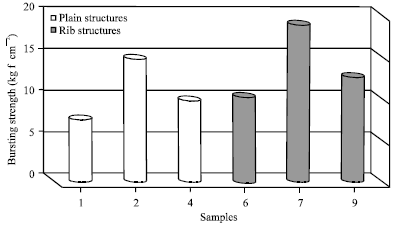
Figure 2 shows the values of bursting strength values (kg f cm-2) of sample No. 1 which presented the composition of 100% cotton plain structure, sample No. 2 which presented the composition of blended plain fabric (50% polyester +50% conductive material), sample No. 4 which presented the composition of blended plain fabric (50% cotton+25% polyester+25% conductive material), sample No. 6 which presented the composition of 100% cotton rib structure, sample No. 7 which presented the composition of blended rib fabric (50% polyester+50% conductive material) and sample No. 9 which presented the composition of blended rib fabric (50% cotton+ 25% polyester+25% conductive material).
 | |
| Fig. 2: | Bursting strength values (kg f cm-2) for different composition samples |
Because of polyester is a strong and flexible material and extremely tear-resistant and is more elastic than cotton, Fig. 2 indicates that blended composition (50% polyester+50% conductive material) for both plain and rib structures causes the best “more” bursting strength properties than all others compositions by using the same other manufacturing parameters.
Based on the results obtained in Fig. 1-2 and by applying the statistics regression, signify that:
| • | Polyester has better bursting strength properties than cotton |
| • | Conductive fibers ratio (%) has a significant effect on bursting strength values for tested samples. As the conductive fibers ratio (%) increases, the bursting strength values increase in produced samples |
| • | Rib structure causes better “more” bursting strength properties than plain structure by using the same conductive fibers ratio (%) because it is production by two sets of needles being alternately set or gated between each other and it is theoretically twice the thickness and half the width of an equivalent plain fabric but it has twice as much width-wise recoverable stretch |
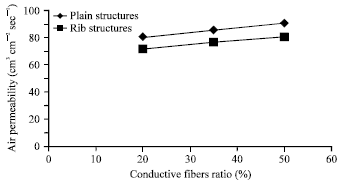
Air permeability: This test was carried out for all samples; Fig. 3 shows the effect of conductive fibers ratio (%) on air permeability values (cm3 cm-2 sec-1) for experimental samples No. (2, 3, 5, 7, 8 and 10).
It is clear that, as shown in Fig. 3, there is difference in air permeability values according to the conductive fibers ratio (%) of produced samples. As the conductive fibers ratio (%) increases, the air permeability values increase in produced samples.
To get a mathematical relationship between the conductive fibers ratio (%) in the plain knitted samples on the air permeability values (cm3 cm-2 sec-1), a linear regression technique was used to get this relationship. The following equation is applied on the air permeability values:
| (3) |
| Y | = | Air permeability values (cm3 cm-2 sec-1) |
| X | = | Conductive fibers ratio (%) |
 | |
| Fig. 3: | Effect of conductive fibers ratio (%) on air permeability values (cm3 cm-2 sec-1) for experimental samples |
As R = 0.9988, the correlation is considered too high which means that the regression equation is reliable for prediction of the air permeability values (cm3 cm-2 sec-1) in the conductive fibers ratio (%) range using plain knitted structure.
To address a mathematical relationship between the conductive fibers ratio (%) in the rib knitted samples on the air permeability values (cm3 cm-2 sec-1), a linear regression equation was used and applied on the air permeability values:
| (4) |
| Y | = | Air permeability values (cm3 cm-2 sec-1) |
| X | = | Conductive fibers ratio (%) |
As R = 0.9996, the correlation is considered too high which means that the regression equation is reliable for prediction of the air permeability values (cm3 cm-2 sec-1) in the conductive fibers ratio (%) range using Rib knitted structure.
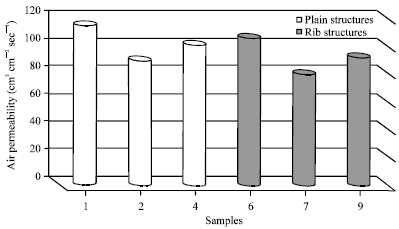
Figure 4 shows the values of air permeability values (cm3 cm-2 sec-1) of sample No. 1 which presented the composition of 100% cotton plain structure, sample No. 2 which presented the composition of blended plain fabric (50% polyester+50% conductive material), sample No. 4 which presented the composition of blended plain fabric (50% cotton+25% polyester+25% conductive material), sample No. 6 which presented the composition of 100% cotton rib structure, sample No. 7 which presented the composition of blended rib fabric (50% polyester+50% conductive material) and sample No. 9 which presented the composition of blended rib fabric (50% cotton+ 25% polyester+25% conductive material).
Because of cotton is breathable material while polyester does not breathe and doesn’t allow air to ventilate as well as cotton does, Fig. 4 indicates that, composition (100% cotton) for both plain and rib structures causes the best “more” air permeability properties than all others compositions by using the same other manufacturing parameters.
Based on the results obtained in Fig. 3-4 and by applying the statistics regression, signify that:
| • | Polyester doesn’t allow air to ventilate as well as cotton does |
| • | Conductive fibers ratio (%) has a significant effect on air permeability values for tested samples. As the conductive fibers ratio (%) increases, the air permeability values increase in produced samples |
| • | Plain knitted structure causes better “more” air permeability properties than rib knitted structure by using the same conductive fibers ratio (%). The existence of this decline is most probably a consequence of the thicker structure of rib fabrics, where the transportation of air through a thick fabric will be difficult while the open structure of the plain fabric knitted gives the ability to the air to pass through fabric without any obstacles |
 | |
| Fig. 4: | Air permeability values (cm3 cm-2 sec-1) for different composition samples |
Water absorption: Water absorption percentage of the fabrics were obtained according to the Eq. 5 and shown in Fig. 5. This test was carried out for all samples; Fig. 5 shows the effect of conductive fiber ratio (%) on the water absorption percentage (%) for experimental samples No. (2, 3, 5, 7, 8 and 10):
| (5) |
It is observed that, as shown in Fig. 5, there is a direct relation between the conductive fibers ratio (%) in the fabric and its water absorption time. As the conductive fibers ratio (%) increases, water absorption percentage (%) decreases in all produced samples.
To get a mathematical relationship between the conductive fibers ratio (%) in the plain knitted samples on the water absorption percentage (%), a linear regression technique was used to get this relationship. The following equation is applied on the water absorption time:
| (6) |
Y | = | Water absorption percentage (%) |
| X | = | Conductive fibers ratio (%) |
As R = -1, the correlation is considered too high which means that the regression equation is reliable for prediction of the water absorption percentage (%) in the conductive fibers ratio (%) range using plain knitted structure.
 | |
| Fig. 5: | Effect of conductive fibers ratio (%) on water absorption (%) for experimental samples |
To address a mathematical relationship between the conductive fibers ratio (%) in the rib knitted samples on the water absorption percentage (%), a linear regression equation was used and applied on the water absorption percentage (%):
| (7) |
| Y | = | Water absorption percentage (%) |
| X | = | Conductive fibers ratio (%) |
As R = -1, the correlation is considered too high which means that the regression equation is reliable for prediction of the water absorption percentage (%) in the conductive fibers ratio (%) range using rib knitted structure.
Figure 6 shows the values of water absorption percentage (%) of sample No. 1 which presented the composition of 100% cotton plain structure, sample No. 2 which presented the composition of blended plain fabric (50% polyester+50% conductive material), sample No. 4 which presented the composition of blended plain fabric (50% cotton+25% polyester+25% conductive material), sample No. 6 which presented the composition of 100% cotton rib structure, sample No. 7 which presented the composition of blended rib fabric (50% polyester+50% conductive material) and sample No. 9 which presented the composition of blended rib fabric (50% cotton+25% polyester+25% conductive material).
Because of polyester isn’t as comfortable as cotton because it keeps sweat close to your body, whereas cotton soaks up and then releases moisture. Unlike cotton, polyester does not breathe and is apt to stick to skin when an individual sweats, Fig. 6 indicates that, composition (100% cotton) for both plain and rib structures causes the best “more” water absorption properties than all others compositions by using the same other manufacturing parameters.
Based on the results obtained in Fig. 5-6 and by applying the statistics regression, indicates that:
| • | Cotton has better absorbency properties than polyester |
| • | Conductive fibers ratio (%) has a significant effect on water absorption percentage (%) for tested samples as the conductive fibers ratio (%) increases it will improve the water proof properties of the fabric |
| • | Rib knitted structure causes better water absorption properties than plain knitted structure by using the same conductive fibers ratio (%). The wick ability rate of interlock structure makes it to have the higher water absorption amount than the SJ. Rib knitted structure can take up the water with higher amount and allow less air passage. These findings indicate that the rib knitted structure can absorb a lot of sweat, perspiration moves fast from skin to outside and as a result user can feel dry and more comfort. Furthermore, rib structures demonstrated the highest water up-take capacity and very high initial wicking rate. This performance is most likely due to the structures' capability to act like a capillary system, rapidly removing and transporting water through the structure. As the fabric becomes tighter, it will have high water absorption capability due to the more fiber material contained and the high fabric thickness accompanied with this fabric specification |
 | |
| Fig. 6: | Water absorption(%) for different composition samples |
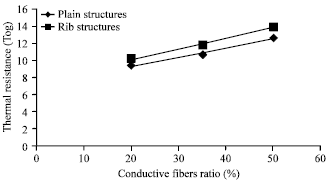
Thermal resistance: The thermal resistance of a batting or batting/fabric system is of considerable importance in determining its suitability for use in fabricating cold weather protective socks systems. The thermal interchange between the human and his environment is, however, an extremely complicated subject which involves many factors in addition to the insulation values of fabrics and battings. Therefore, measured thermal insulation values can only indicate relative merit of a particular material. This test was carried out for all samples; Fig. 7 shows the effect of conductive fibers ratio (%) on the thermal resistance values (Tog) for experimental samples No. (2, 3, 5, 7, 8 and 10).
It is observed that, as shown in Fig. 7, there is a direct relation between the conductive fibers ratio (%) in the fabric and its thermal resistance properties. As the conductive fibers ratio (%) increases, thermal resistance values increase in all produced samples.
To get a mathematical relationship between the conductive fibers ratio (%) in the plain knitted structure samples on the thermal resistance values, a linear regression technique was used to get this relationship. The following equation is applied on the thermal resistance values:
| (8) |
| Y | = | Thermal resistance values |
| X | = | Conductive fibers ratio (%) |
 | |
| Fig. 7: | Effect of conductive fibers ratio (%) on thermal resistance values (Tog) for experimental samples |
As R = 0.9796, the correlation is considered too high which means that the regression equation is reliable for prediction of the thermal resistance values in the conductive fibers ratio (%) range using plain knitted structure.
To address a mathematical relationship between the conductive fibers ratio (%) in the rib knitted structure samples on the thermal resistance values, a linear regression equation was used and applied on the thermal resistance values:
| (9) |
| Y | = | Thermal resistance values |
| X | = | Conductive fibers ratio (%) |
As R = 0.9939, the correlation is considered too high which means that the regression equation is reliable for prediction of the thermal resistance values in the conductive fibers ratio (%) range using Rib knitted structure.
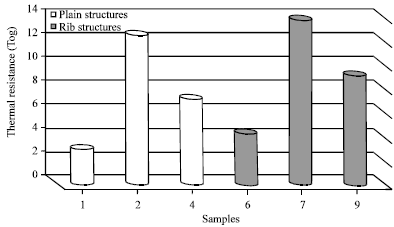
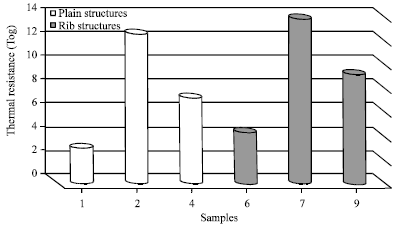
Figure 8 shows the values of thermal resistance values (Tog) of sample No. 1 which presented the composition of 100% cotton plain structure, sample No. 2 which presented the composition of blended plain fabric (50% polyester+50% conductive material), sample No. 4 which presented the composition of blended plain fabric (50% cotton+25% polyester+25% conductive material), sample No. 6 which presented the composition of 100% cotton rib structure, sample No. 7 which presented the composition of blended rib fabric (50% polyester+50% conductive material) and sample No. 9 which presented the composition of blended rib fabric (50% cotton+25% polyester+25% conductive material).
Because of copper fibers are thermal regulating, they hold body heat emanating from within and redirect this warmth back to the body, Fig. 8 indicates that, composition of blended fabric (50% polyester+50% conductive material) for both plain and rib structures causes the best “more” thermal resistance properties than all others compositions by using the same other manufacturing parameters.
Based on the results obtained in Fig. 7-8 and by applying the statistics regression, signify that:
| • | Copper fibers have better conductive and thermal insulating properties than polyester and cotton |
| • | Conductive fibers ratio (%) has a significant effect on thermal resistance values for tested samples. As the conductive fibers ratio (%) increases, thermal resistance values increase in all produced samples |
| • | Rib knitted structure causes better “more” thermal insulation properties than plain knitted structure samples by using the same conductive fibers ratio (%). This case can be explained by the high bulk density; high weight per square meter and less still air in the unit area of rib knitted structures. Moreover, in plain knitted structure the thermal conductivity decreases. This could be referred to higher porosity value and the less fabric weight of the plain knitted structure |
 | |
| Fig. 8: | Thermal resistance values (Tog) for different composition samples |
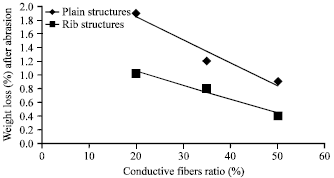
Fabric weariness or abrasion: This test was carried out for all samples; Fig. 9 shows the effect of conductive fiber ratio (%) on their weight loss values (%) after abrasion (100 cycles) for experimental samples No. (2, 3, 5, 7, 8 and 10).
It is observed that, as shown in Fig. 9, there is a direct relation between the conductive fibers ratio (%) in the fabric and its weight loss values (%) after abrasion. As the conductive fibers ratio (%) increases, weight loss values (%) after abrasion decrease in all produced samples.
To get a mathematical relationship between the conductive fibers ratio (%) in the plain knitted structure samples on the weight loss values (%) after abrasion, a linear regression technique was used to get this relationship. The following equation is applied on the weight loss values (%) after abrasion:
| (10) |
| Y | = | The weight loss values (%) after abrasion |
| X | = | Conductive fibers ratio (%) |
As R = -0.9494, the correlation is considered too high which means that the regression equation is reliable for prediction of the weight loss values (%) after abrasion in the conductive fibers ratio (%) range using plain knitted structure.
To address a mathematical relationship between the conductive fibers ratio (%) in the rib knitted structure samples on the weight loss values (%) after abrasion, a linear regression equation was used and applied on the weight loss values (%) after abrasion:
 | |
| Fig. 9: | Effect of conductive fibers ratio (%) on their weight loss values (%) after abrasion for experimental samples |
| (11) |
| Y | = | Weight loss values (%) after abrasion |
| X | = | Conductive fiber ratio (%) |
As R = - 0.9727, the correlation is considered too high which means that the regression equation is reliable for prediction of the weight loss values (%) after abrasion in the conductive fibers ratio (%) range using rib knitted structure.
Fig. 10 shows the values of weight loss values (%) after abrasion of sample No. 1 which presented the composition of 100% cotton plain structure, sample No. 2 which presented the composition of blended plain fabric (50% polyester+50% conductive material), sample No. 4 which presented the composition of blended plain fabric (50% cotton+25% polyester+25% conductive material), sample No. 6 which presented the composition of 100% cotton rib structure, sample No. 7 which presented the composition of blended rib fabric (50% polyester+50% conductive material) and sample No. 9 which presented the composition of blended rib fabric (50% cotton+ 25% polyester+25% conductive material).
Because of copper fibers and polyester have better durability properties compared with cotton, Fig. 10 indicates that, composition of blended fabric (50% polyester+50% conductive material) for both plain and rib structures causes the best “more” abrasion resistance properties than all others compositions by using the same other manufacturing parameters.
Based on the results obtained in Fig. 9 and 10 by applying the statistics regression, signify that:
| • | Copper fibers and polyester have better abrasion resistance properties compared with cotton |
| • | Conductive fibers ratio (%) has a significant effect on the weight loss values (%) after abrasion for all tested samples. As the conductive fibers ratio (%) increases, weight loss values (%) after abrasion decrease in all produced samples |
| • | Rib knitted structure causes better abrasion resistance properties than plain knitted structure samples by using the same conductive fibers ratio (%). This case can be explained by the high bulk density; high weight per square meter of rib knitted structures |
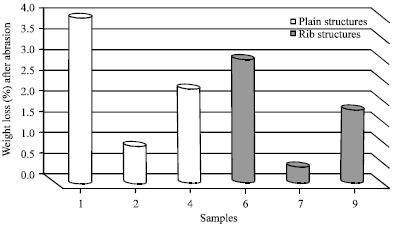 | |
| Fig. 10: | Weight loss values (%) after abrasion for different composition samples |
| Table 4: | Comparison of growth rate of bacteria and fungi |
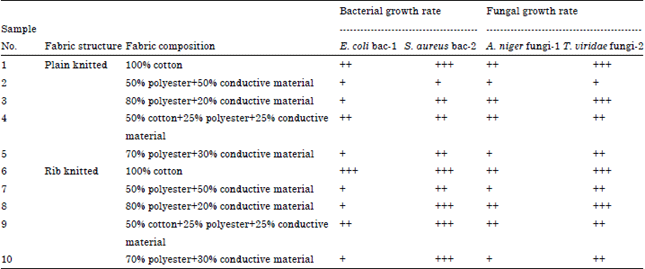 | |
| +: Moderate growth rate, ++: High growth rate | |
Determination the growth rate of bacteria (E. coli and S. aureus) and fungi (T. viridae and A. niger): The growth rate of bacteria (E. coli and S. aureus) and fungi (T. viridae and A. niger) were compared when grown on the ten test samples as substrates. The results are presented in Table 4. This test proves that the growth rate of organisms on copper or conductive fibers as a substrate is less, when compared with cotton and polyester. The natural antimicrobial effect of copper does not allow the multiplication of bacteria and fungi and ultimately proves to be both bacteria static and fungi static. The growth rate of microorganisms on Plain knitted structure is less when compared with rib knitted structure.
This test proves that copper effectively kills a broad spectrum of viruses, bacteria and fungus, from exposure to copper ions. Copper oxide releases ions that penetrate the harmful bacteria/fungus causing:
| • | Membrane rupture, causing loss of basic nutrients and fluid |
| • | Damage to microbe genetic material such as DNA and RNA |
| • | Damage to proteins |
| • | It does not allow reproduction of bacteria/fungi |
This study presents a quantitative study of various functional properties carried out on different knitted fabric structures (Rib-Jersey) containing conductive fibers with various ratios (%) and aiming at the selection the most adequate fabric for socks applications. From the results obtained it can be concluded that the performance and functional properties of the studied fabrics is greatly affected by the ratio of conductive fibers (%) which significantly increased or decreased the values of the different comfort related properties evaluated.
Combinations of cotton, polyester and conductive fibers gave socks better functional properties than a single fiber type with greatest performance properties. On the basis of the results obtained it could be concluded that the cobber fibers ratio (%) in socks has a significant effect on improving the thermal conductivity, anti-microbial behavior, abrasion resistance, bursting strength and air permeability properties for both plain and rib structures. Based on the pervious in-depth analysis, it was observed that cobber fibers have good antimicrobial properties. This indigenous anti microbial property of cobber fibers makes it more suitable for foot wears such as socks as compared to ordinary fibers.
The results indicated that plain knitted structures have less thermal conductivity, abrasion resistance, water absorption, bursting strength properties and better air permeability, water vapor permeability properties and anti-microbial behavior than rib knitted structures by using the same conductive fibers ratio (%). This case can be clarified by the high amount of entrapped air inside the plain knitted structures because of its higher porosity value and their lower weight per square meter and thickness, respectively. In the other side, rib knitted structures the high bulk density; high weight per square meter and less still air in the unit area.
All previous findings are an important tool in the design of healthy comfortable socks.