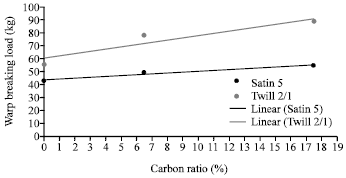
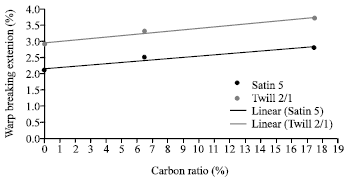
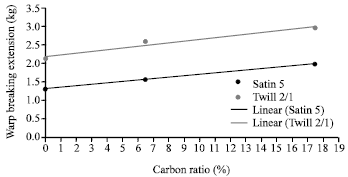
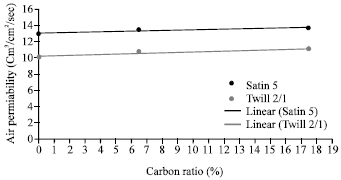
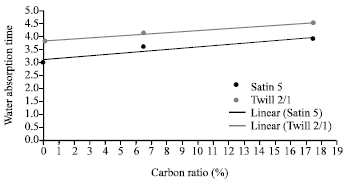
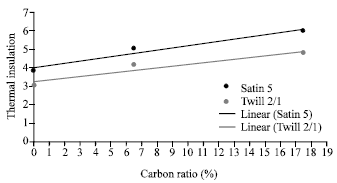
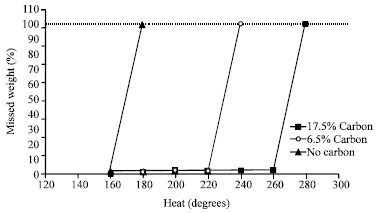
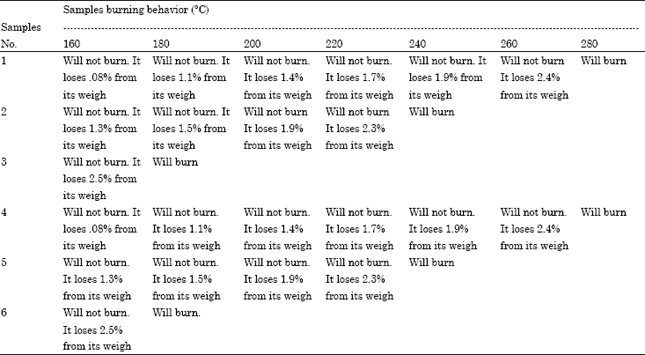
Research Article
Enhancing the Functional Properties of Sportswear Fabric based Carbon Fiber
Department of Spinning, Weaving and Knitting, Faculty of Applied Arts, Helwan University, Giza, Egypt
R.A.A. Abd El-Baky
Department of Spinning, Weaving and Knitting, Faculty of Applied Arts, Helwan University, Giza, Egypt