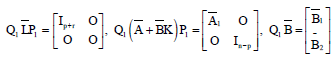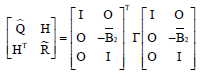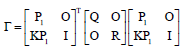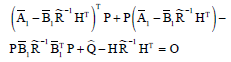Research Article
On the LQ Optimization Subject to Descriptor System under Disturbance
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Andalas, Kampus Unand Limau Manis, 25163 Padang, Indonesia
Narwen
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Andalas, Kampus Unand Limau Manis, 25163 Padang, Indonesia
Budi Rudianto
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Andalas, Kampus Unand Limau Manis, 25163 Padang, Indonesia
Ahmad Iqbal Baqi
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Andalas, Kampus Unand Limau Manis, 25163 Padang, Indonesia
Muhafzan
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Andalas, Kampus Unand Limau Manis, 25163 Padang, Indonesia
LiveDNA: 62.20729