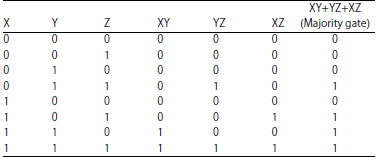
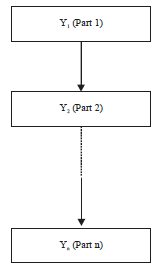
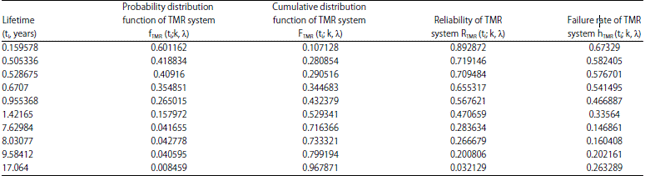
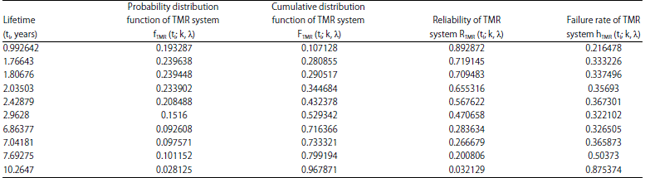
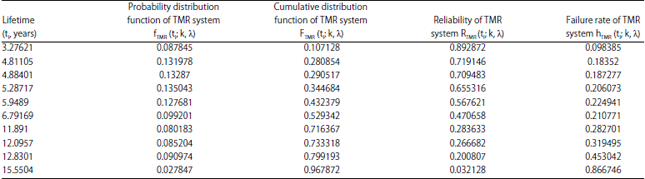
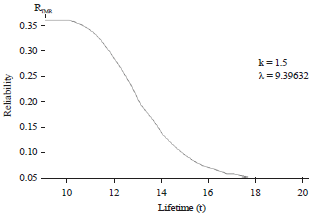
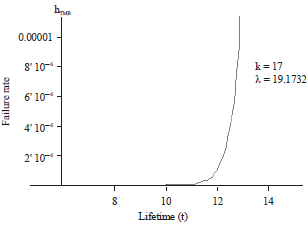
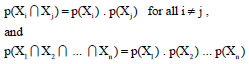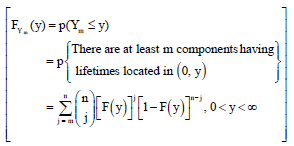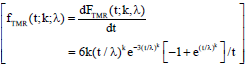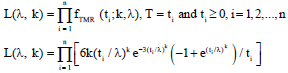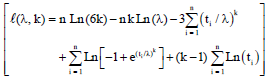Research Article
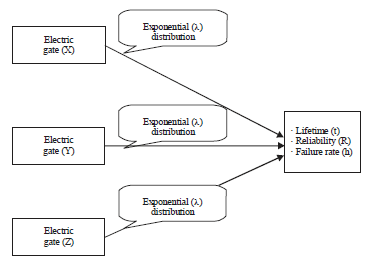
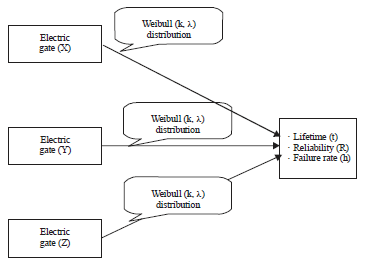
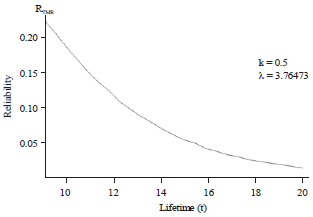
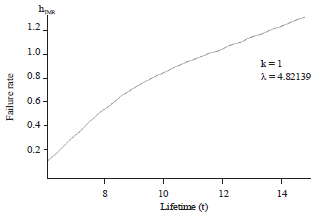
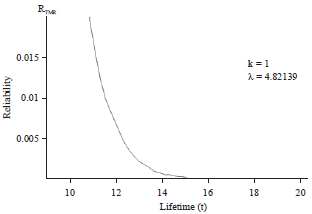
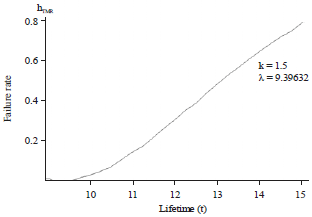
Estimation the Failure Rate and Reliability of the Triple Modular Redundancy System Using Weibull Distribution
Department of Mathematics and Computer Science, Faculty of Science, Port Said University, Port Said, Egypt
LiveDNA: 20.4959
Esraa Ahmed Hebeshy
Department of Mathematics and Computer Science, Faculty of Science, Port Said University, Port Said, Egypt