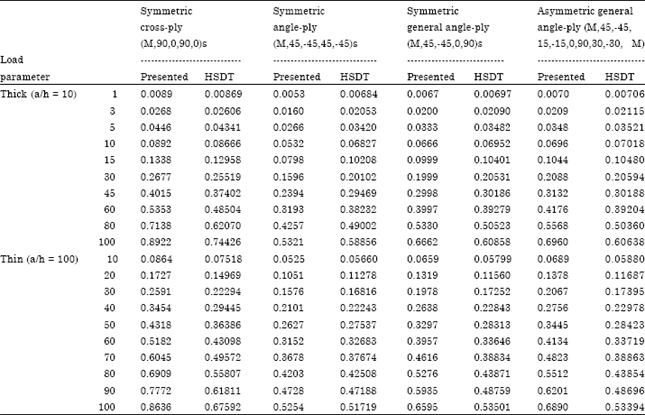
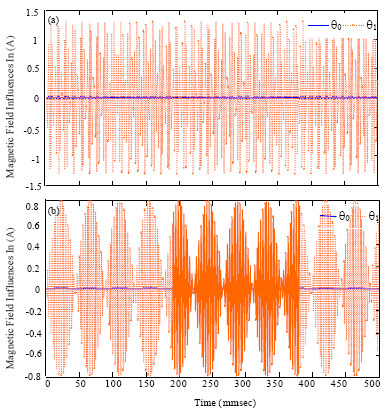
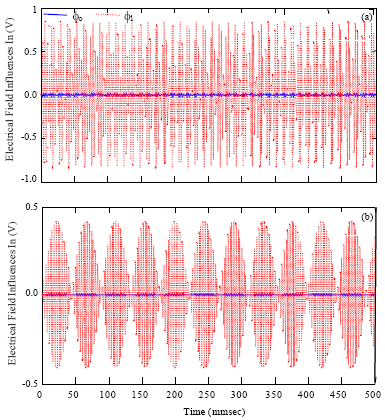
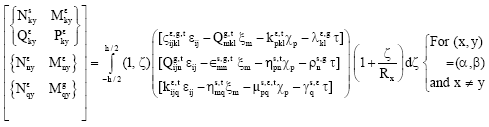Research Article
Analytical Solution for Simply Supported and Multilayered Magneto-Thermo-Electro-Elastic Plates
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Hussain H. Al-Kayiem
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia