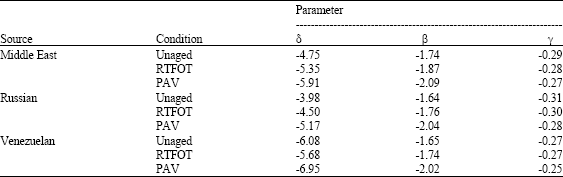
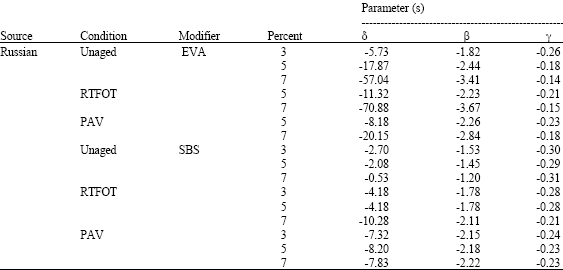
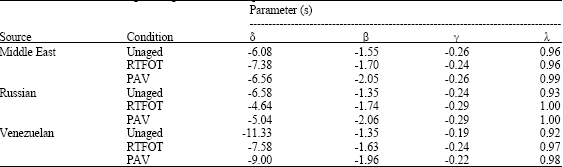
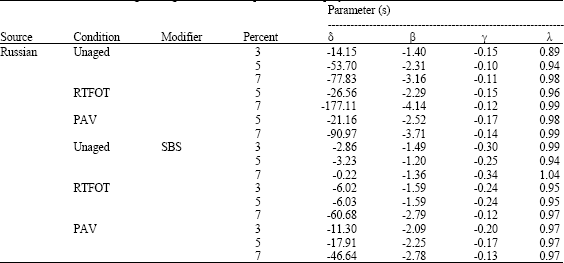
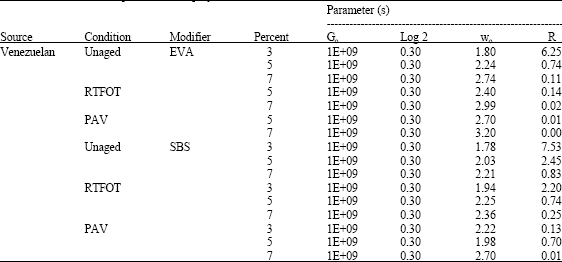
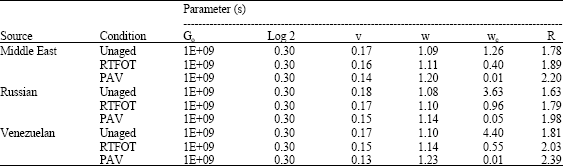
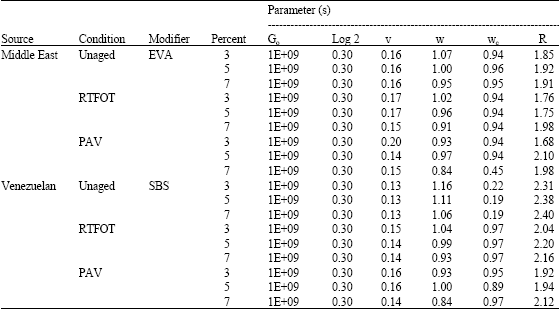
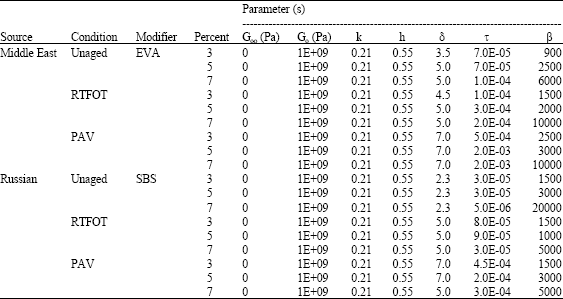
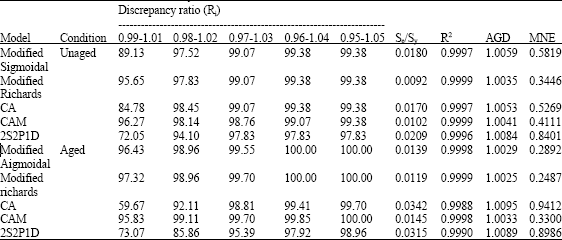
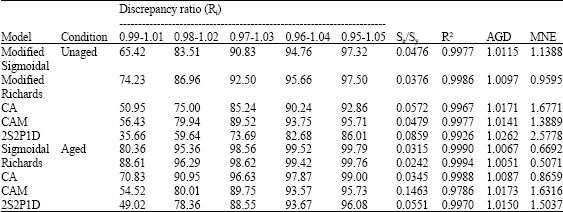
Research Article
Predictability of Complex Modulus Using Rheological Models
Nottingham Transportation Engineering Centre, School of Civil Engineering, University of Nottingham, University Park, NG7 2RD, Nottingham, United Kingdom
G.D. Airey
Nottingham Transportation Engineering Centre, School of Civil Engineering, University of Nottingham, University Park, NG7 2RD, Nottingham, United Kingdom
M.R. Hainin
Faculty of Civil Engineering, Universiti Teknologi Malaysia, 81310 UTM Skudai, Johor, Malaysia