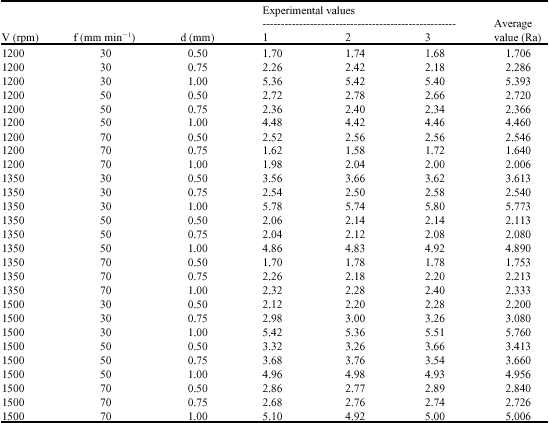
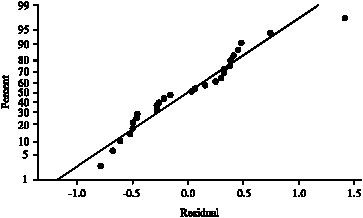
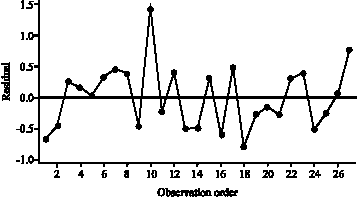
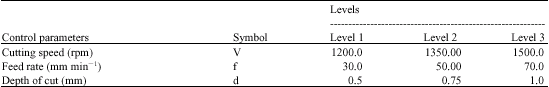Research Article
Surface Roughness Prediction Techniques for CNC Turning
Department of Mechanical Engineering, R.G.M. College of Engineering and Technology, Nandyal, Kurnool (Dt), Andhra Pradesh, 518501, India
G. Padmanabhan
Department of Mechanical Engineering, Sri Venkateswara University, College of Engineering, S.V. University, Tirupati, India
K. Vijay Kumar Reddy
Director of Evaluation of J.N.T. University, Hyderabad, Andhra Pradesh, India