ABSTRACT
Calculations of Millimeter-wave rain scattering parameters are made at 16, 19.3 and 34.8 using spherical and oblate spheroidal rain models. Computations are made at angle of incidence of 0 and 90 ° for the oblate spheroidal rain model. The characteristic of the difference between the two models with rain rate are studied at incidence angle of 0 ° to allow us determine their suitability in a tropical environment. Some propagation parameters are evaluated using the Indian lognormal and Marshall and Palmer (MP) Drop Size Distributions (DSD’s). Marshall and Palmer DSD model could underestimate rain-induced attenuation at all the frequencies in the rain rate range of 0.25≤R<50 mm h-1 and overestimate specific phase shift at rain rate R>100 mm h-1 if adopted for radio wave propagation prediction on tropical path. However, Indian data compare well with MP at rain rate in the range 50≤R≤100 mm h-1. Similarly, spherical rain model could underestimate the specific attenuation with a maximum margin of 3.4 dB km-1 at 34.8 GHz and specific phase shift of 15.7 ° km-1 at 16 GHz, both at rain rate of 150 mm h-1. The empirical scaling relationship between the radar reflectivity η and rain rate R (η = aRb) are derived for the Indian DSD and the coefficients a and b compare well with those of Aydin and Lure.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ajsr.2008.213.221
URL: https://scialert.net/abstract/?doi=ajsr.2008.213.221
INTRODUCTION
It is well recognized that rain is the major factor that adversely affect the propagation of electromagnetic wave signals especially at frequencies above 10 GHz. The knowledge of its scattering characteristics in a location of interest is therefore very crucial in the engineering of reliable communication system. Scattering properties of oblate spheroidal at both horizontal and vertical polarizations are very important in the estimation of crosstalk. The feasibility of using orthogonal polarizations to increase channel capacity in both satellite and terrestrial systems depends on the cross polarization isolation that is obtainable under worst-case system operating conditions (Oguchi, 1980).
There have been significant contributions to the study of interaction between raindrop and the incident electromagnetic waves using temperate data (for a partial list, see references cite in Oguchi, 1980, 1986, 1991). However, a few authors (Ajayi and Ofuche, 1984; Ajewole et al., 1999) have investigated the study of interaction of radio signals with tropical rain data, which had contributed to the reason for dearth rain-induced impairments data for the tropics especially over Indian continent (Kunhikrishnan et al., 2006). Verma and Jha (1996) had earlier reported the Indian lognormal Drop Size Distribution (DSD) and comparison was made with those of Nigeria and Brazil.
This paper reports the result obtained from the computation of the scattering parameters using Indian lognormal drop size distribution of Verma and Jha (1996) at frequencies of 16, 19.3 and 34.8 GHz for spherical and oblate spheroidal rain models. The computations are performed with the Mie theory technique for the spherical rain model while empirical relation connecting the attenuation and phase shift with propagation constant of Oguchi (1983) was employed for the oblate spheroidal rain model. The spherical raindrops assumed temperature of 20 ° and their refractive index and propagation constant at this temperature are calculated at the chosen frequencies using the model reported in Ray (1972). The characteristics of rain-induced impairments with spherical rain model do not depend on the polarization of the incident wave or on the angle of incidence while calculations using oblate spheroidal rain model are performed at angle of incidence of 0 and 90 ° to the surface of the raindrop. The scattering parameters at incidence angle of 0 ° are the same for horizontal and vertical polarizations with oblate spheroidal rain model. On this basis, the results with spherical and oblate spheroidal rain models are compared at incidence angle of 0 °. The frequency characteristics of the differential attenuation and differential phase shift for the two orthogonal linear polarizations are investigated. Radar reflectivity for spherical rain model and its variation with rain rate and frequency are studied. The coefficients of the power law relationship between the radar reflectivity and rain rate are derived and this have direct dependence on the drop size distribution employed which invariably reflects the influence of climatic on the electromagnetic waves as it propagates.
COMPUTATIONAL PROCEDURE OF THE SCATTERING PARAMETERS
The scattering computations were performed using the generalized lognormal drop size distributions of the form
(1) |
It represents the number of drops, N, of diameter D in unit volume, it follows therefore that N(D) is the number of drops per unit volume per diameter interval, μ is the mean of ln (D), σ is the standard deviation and NT is the number of drops of all sizes. The parameter of the lognormal; μ, σ and NT for the Indian region credited to Verma and Jha (1996) is:
| NT μ σ2 | = 169.05R0.2937 = -0.05556 + 0.130961 InR = 0.30042 - 0.023604 InR | (2) |
The correlation coefficient is better than 0.95 and standard error of correlation coefficient is less than 0.0015. The raindrop size distribution are calculated for 13 equivolume raindrops with radii in the range 0.25-3.25 mm at rain rates varying from 0.25-150 mm h-1.
The backscattering cross section QB integrated over the drop size distribution N (D) leads to the radar reflectivity (Aydin and Lure, 1991) which is express as:
(3) |
QB is defined as the backscattering cross section, it is express as:
(4) |
The nth electric partial wave has amplitude an and bn is the magnitude of the nth magnetic partial wave and q = k0a = 2πna/λ. Basic equations relevant in the computation of scattering parameters using Mie theory has been reported in Adekola (2002). Calculations of radar reflectivity are performed for spherical rain model at all the frequencies considered in this study and the power law relation between the radar reflectivity and rain rate are derived.
The Attenuation, A in dB and the Phase shift, Φ in degrees for two characteristics polarizations are given by Oguchi (1981).
AH,V = 8.686 Im (kH,VL) | (5) |
(6) |
Where:
| L | = | The propagation path length, |
| kH,V | = | The propagation constant. |
Assuming that plane waves with electric fields polarized in the horizontal and vertical directions are incident on the rain medium, Oguchi (1966) earlier proposed an expression for the propagation constant given as:
(7) |
Where:
| fH,V (0) | = | The scattering amplitude functions of a raindrop with diameter D in the forward direction and for horizontal and vertical polarizations, |
| k0 | = | The free-space wave number. |
Calculation of attenuation and phase shift are done at propagation path length of 1 km.
RESULTS AND DISCUSSION
The calculations are performed for spherical and oblate spheroidal rain models at 16, 19.3 and 34.8 GHz frequencies and at rain rate between 0.25 and 150 mm h-1 based on scattering by single particle and based on tropical lognormal drop size distribution of India region. The chosen frequencies are of practical importance to terrestrial and earth-satellite communication systems. The results of the calculation for spherical rain model do not depend on the polarization of the incident wave or on the angle of incidence while calculations using oblate spheroidal rain model are performed at angle of incidence of 0 and 90 ° to the surface of the raindrop. Also note that the scattering parameters at incidence angle of 0 ° are the same for horizontal and vertical polarizations. This gives an avenue for comparison between the results using spherical and oblate spheroidal rain models since there is no difference between horizontal and vertical polarized scattering parameters when spherical rain model is assumed.
The results of specific attenuation and specific phase shift are shown in Table 1 for spherical rain model at 16, 19.3 and 34.8 frequencies and Table 2-4 for oblate spheroidal rain model at 16, 19.3 and 34.8 GHz, respectively. The specific attenuation and specific phase shift in both polarizations becomes very large as the rain rate increase and as frequency also increases. This is an indication that increase in the frequency of the radio signal propagated through rain medium will deteriorate the quality of the signal at the receiver end. High rain rate will also adversely affect the radio signal in the same way.
| Table 1: | Specific attenuation and specific phase shift using spherical rain model based on tropical lognormal drop size distribution and comparison with Marshall and palmer |
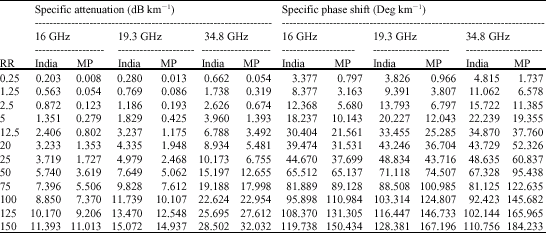 | |
| MP: Marshall and Palmer; RR: Rain rate in mm h-1 | |
| Table 2: | Specific attenuation and specific phase shift of vertically and horizontally polarized wave at frequency of 16 GHz for 1 km propagation path based on tropical lognormal drop size distribution and comparison with Marshall and palmer |
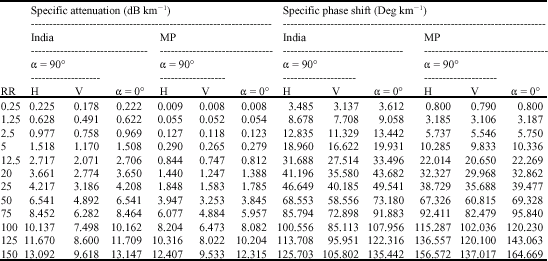 | |
| H: Horizontal polarization; V: Vertical polarization; α: Angle of incidence; MP: Marshall and Palmer; RR: Rain rate in mm h-1 | |
| Table 3: | Specific attenuation and specific phase shift of vertically and horizontally polarized wave at frequency of 19.3 GHz for 1 km propagation path based on tropical lognormal drop size distribution and comparison with Marshall and palmer. |
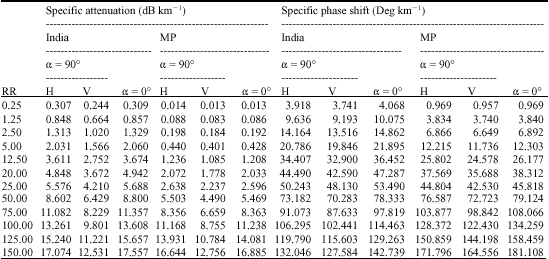 | |
| H: Horizontal polarization; V: Vertical polarization; α: Angle of incidence; MP: Marshall and Palmer; RR: Rain rate (mm h-1) | |
| Table 4: | Specific attenuation and specific phase shift of vertically and horizontally polarized wave at frequency of 34.8 GHz for 1 km propagation path based on tropical lognormal drop size distribution and comparison with Marshall and palmer |
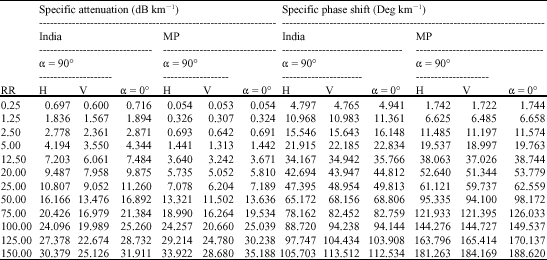 | |
| H: Horizontal polarization; V: Vertical polarization; α: Angle of incidence; MP: Marshall and Palmer; RR: Rain rate (mm h-1) | |
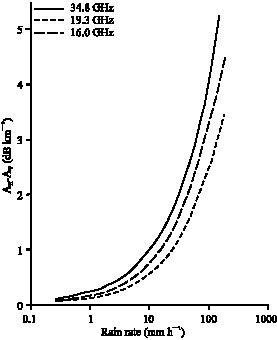
Calculations of scattering impairments by rain in the tropical climates are therefore crucial since high rain rate are experienced in this region. The results presented also show that specific attenuation and specific phase shift are very dependence on the polarization. Radio signals experience more attenuation and absorption in the horizontal than in the vertical polarization. The difference between specific attenuation and specific phase shift based on Oblate spheroidal and spherical rain models are presented in Fig. 1 and 2, respectively. The difference in the specific attenuation increases with the rain rate at all the frequencies considered. It also increases with frequency for a fixed rain rate. Interestingly, the difference in phase shift at 16 and 19.3 becomes very large as the rain rate increase whereas the corresponding value at 34.8 GHz is within a very small range of angles throughout all the rain rates considered. This implies that spherical rain model has the tendency to underestimate rain-induced impairments when assumed in the propagation prediction on tropical path.
Figure 3 shows that the differential attenuation in both polarizations at all the frequencies considered and become very large as the rain rate increase; however it decreases with increase in frequency for a fixed rain rate. These are very important in the estimation of crosstalk in the design of radio communication systems, which is outside the scope of this work. Comparing the Indian data with those of Marshall and Palmer (1948) shows that their difference is not serious but comparatively higher at rain rates between 0.25 and 25 mm h-1 within 2.9 dB km-1 for specific attenuation and 10 deg km-1 for specific phase shift.
 | |
| Fig. 1: | Difference between the specific attenuation obtained from Oblate spheroidal and spherical rain models as a function of the rain rate based on the India drop size distribution at angle of incidence of 0° |
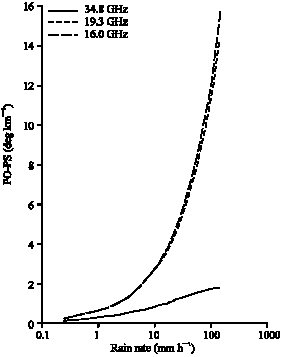 | |
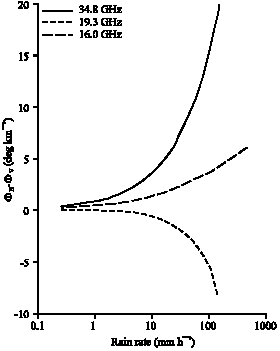
| Fig. 2: | Difference between the specific phase shifts obtained from Oblate spheroidal and spherical rain models as a function of the rain rate based on the India drop size distribution at angle of incidence of 0° |
 | |
| Fig. 3: | Differential attenuation (ΔA = AH-AV) obtained using Oblate spheroidal rain model as a function of the rain rate based on the Indian drop size distribution |
 | |
| Fig. 4: | Differential phase shift (ΔΦ = ΦH-ΦV) obtained using Oblate spheroidal rain model as a function of the rain rate based on the Indian drop size distribution |
Note that the phase rotation at rain rate of 150 mm h-1 for instance is greater at frequency of 19.3 GHz than at frequency of 16 GHz whereas it reduces at frequency of 34.8 GHz.
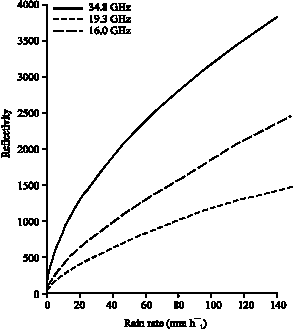 | |
| Fig. 5: | Reflectivities obtained from spherical rain model as a function of the rain rate based on the Indian drop size distribution |
| Table 5: | Power law relationship between Radar Reflectivity (η) and Rain rate obtained using the lognormal drop size distribution for spherical rain model and its comparison with those of Marshall and Palmer with oblate spheroidal rain model |
 | |
| F: Frequency GHz; 2Aydin and Lure for side incidence; 3Aydin and Lure for vertical incidence; The results are at horizontal polarization using Marshall and Palmer (MP), Joss Drizzle (J-D) and Joss Thunderstorm (J-T) drop size distribution | |
This is an indication that there is a peak frequency at which highest amount of phase rotation is experienced by radio signal as it is transmitted through the rain medium at 25 GHz for the Indian region. The differential phase shift as a function of rain rate is shown in Fig. 4. It also increase with the rain rate, however it decreases with frequency for a fixed value of rain rate. An exception to this result occurs for 34.8 GHz where the difference decreases rapidly to negative values.
The reflectivity generally increases with rain rate at all the frequency (Fig. 5). Empirical scaling relationship can be employed to estimate radar reflectivity for practical engineering application. The results obtained are used to obtain the parameters of the empirical approximation and this is shown in Table 5. Aydin and Lure (1991) earlier reported results of their computation at 94 and 140 GHz using Marshall and Palmer, Joss drizzle and Joss thunderstorm drop size distribution. The present result is therefore compared with those of Aydin and Lure (1991) at 94 and 140 GHz frequencies, though our computations are for spherical rain model but result for horizontal polarization of Oblate spheroidal rain model are reported by Aydin and Lure (1991), still, they compare well with those of Marshall and Palmer at 94 GHz.
CONCLUSIONS
In this study, scattering parameters of spherical and oblate spheroidal rain models are calculated using the Indian lognormal DSD and compared with MP DSD. Though MP DSD could underestimate specific attenuation and overestimate specific phase shift at some rain rates, however the Indian data still compared well at some other rain rate. The degree of suitability of assuming spherical rain model for rain-induced impairments prediction in tropical environment are reported. It was observed that spherical rain model could underestimate rain-induced impairments in a tropical path. The dependence of specific attenuation and specific phase shift on polarization are also investigated. Radio signal suffers more attenuation and phase rotation in the horizontal than in the vertical polarization. The coefficients of the power law relationship between the radar reflectivity and rain rate reported in this paper agree well with those of Aydin and Lure (1991).
REFERENCES
- Ajayi, G.O. and B.C. Ofoche, 1984. Some tropical rate characteristics at Ile-Ife for microwave and millimeter wave applications. J. Climate Applied Meteorol., 23: 562-567.
CrossRef - Ajewole, M.O., L.B. Kolawole and G.O. Ajayi, 1999. Theoretical study of effect of different types of tropical rainfall on microwave and millimeter-wave propagation. Radio Sci., 34: 1103-1124.
Direct Link - Aydin, K. and Y. Lure, 1991. Millimeter wave scattering and propagation in rain: A computational study at 94 and 140 GHz for oblate spheroidal and spherical raindrops. IEEE Trans. Geosci. Remote Sen., 29: 593-601.
CrossRef - Marshall, J. S. and W. M. K. Palmer, 1948. The distribution of raindrops with size. J. Meteor., 5: 165-166.
CrossRef - Oguchi, T., 1980. Effect of incoherent scattering on attenuation and cross-polarization of millimeter-waves due to rain: Preliminary calculations at the 34.8 and 82 GHz for spherical raindrops. Ann. Telecommun., 35: 380-389.
CrossRefDirect Link - Oguchi, T., 1981. Summary of studies on scattering of centimeter and millimeter waves due to rain and hail. Ann. Telecommun., 36: 383-399.
CrossRefDirect Link - Oguchi, T., 1983. Electromagnetic wave propagation and scattering in rain and other hydrometeors. Proc. IEEE, 17: 1029-1078.
Direct Link - Oguchi, T., 1986. Effect of incoherent scattering on attenuation and depolarization of millimeter and optical waves due to hydrometeors. Radio Sci., 21: 717-730.
Direct Link - Oguchi, T., 1991. Effect of incoherent scattering on microwave and millimeter wave communications through rain. Electron Lett., 27: 759-760.
CrossRef - Ray, P.S., 1972. Broadband complex refractive indices of ice and water. Applied Optics, 11: 1836-1844.
Direct Link








