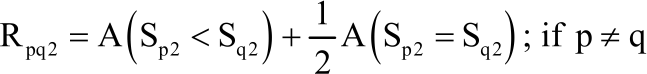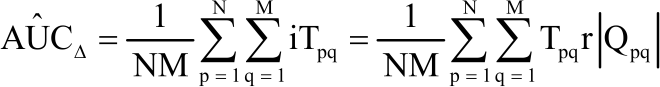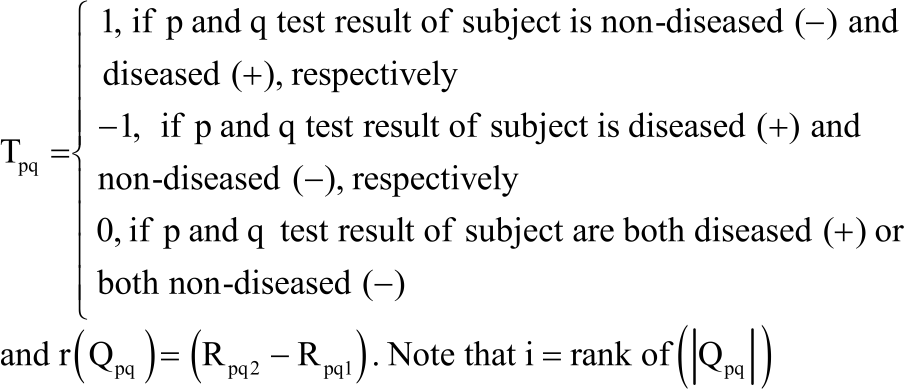Research Article
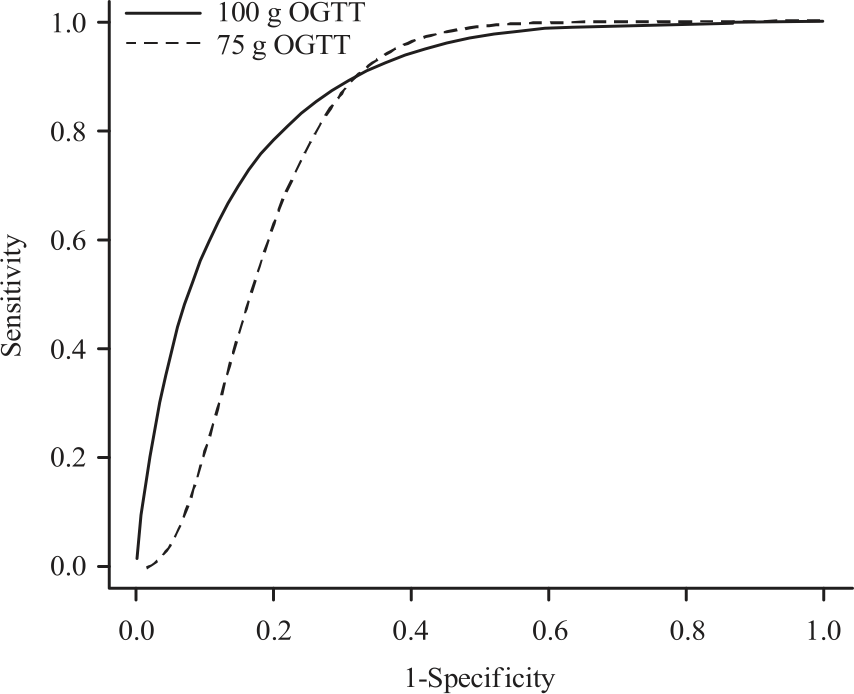
Comparison of Two Diagnostic Test Procedures Using Modified Wilcoxon Signed Rank Test
Department of Industrial Mathematics and Applied Statistics, Ebonyi State University, Abakaliki, Nigeria
LiveDNA: 234.16012
I. Onyeagu Sidney
Department of Statistics, Nnamdi Azikiwe University Awka, Anambra, Nigeria