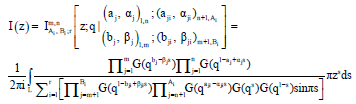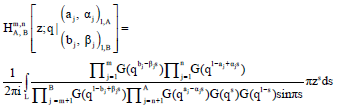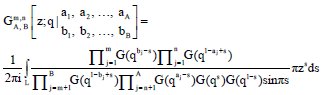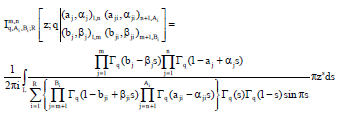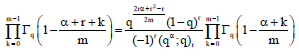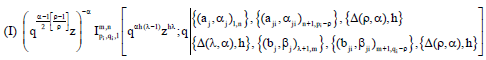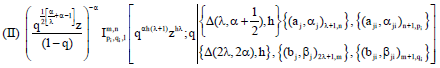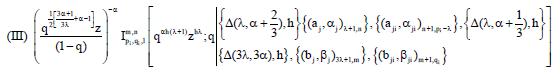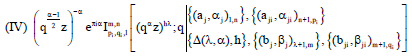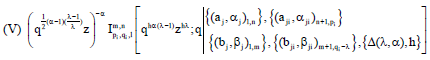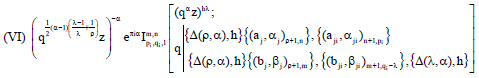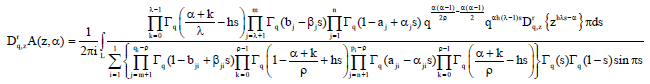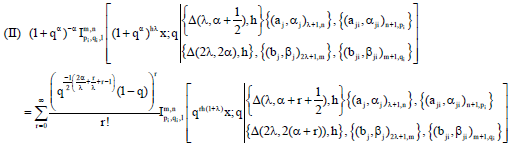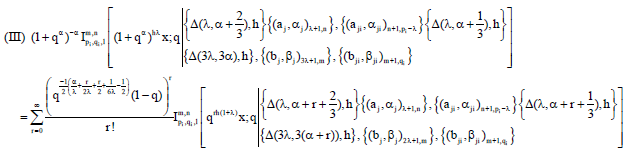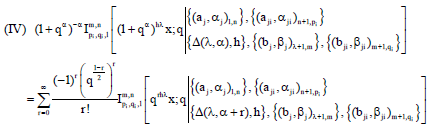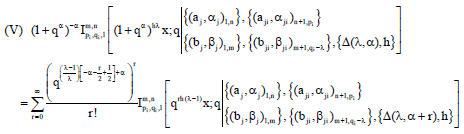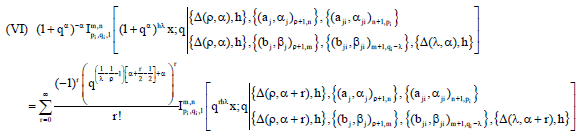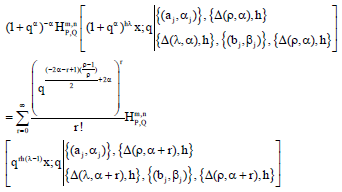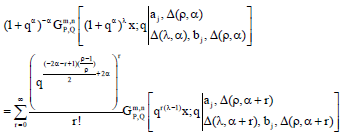Research Article
Generating q-Analogue of I-Function Satisfying Truesdell's Ascending Fq-Equation
School of Mathematics and Allied Sciences, Jiwaji University, Gwalior (M.P.), India
LiveDNA: 91.24683
Renu Jain
School of Mathematics and Allied Sciences, Jiwaji University, Gwalior (M.P.), India
Deepak Kumar Jain
Department of Applied Mathematics, MITS, Gwalior (M.P.), India