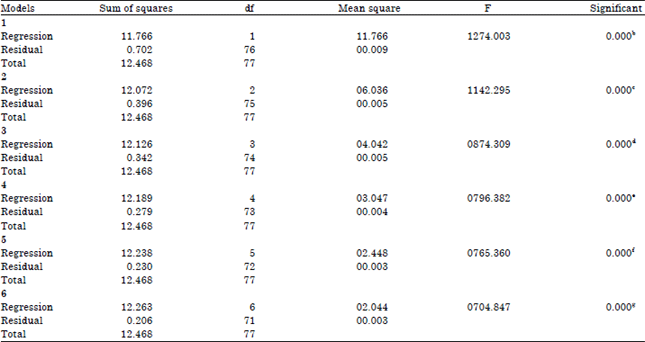
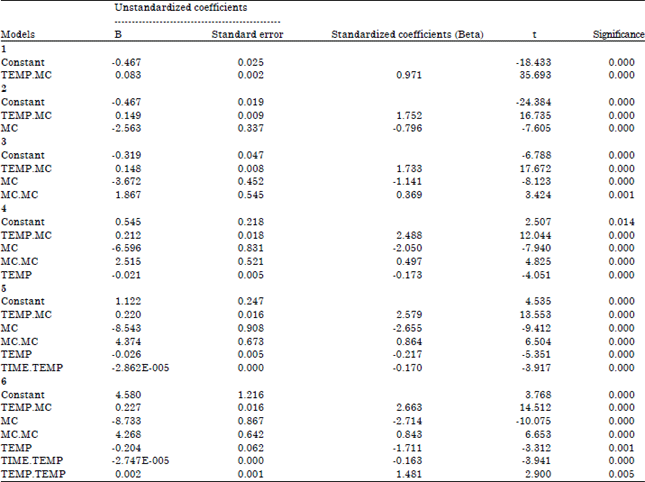
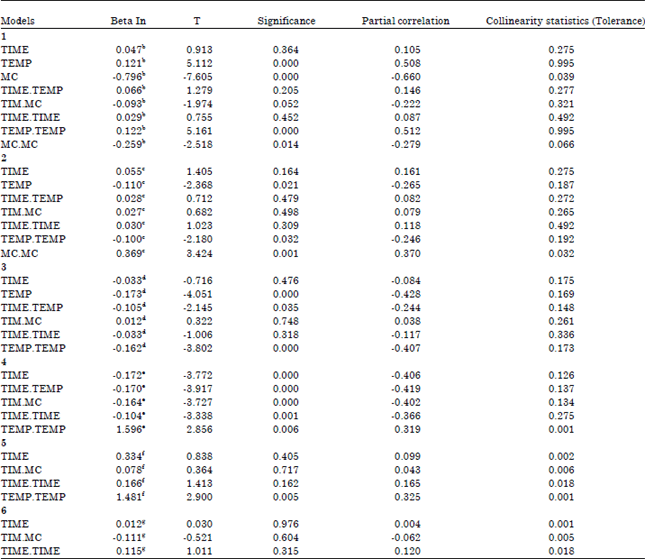
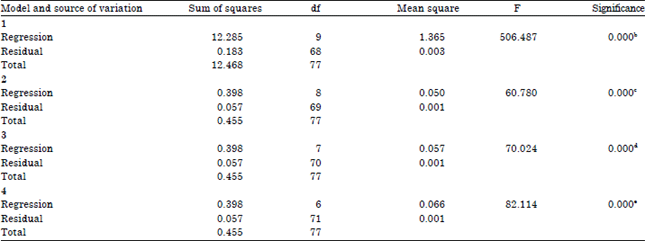
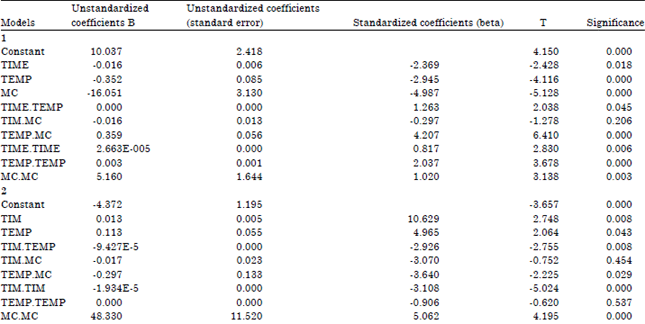
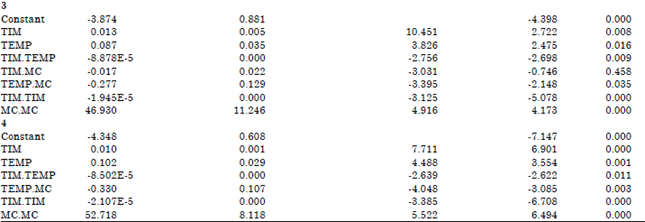
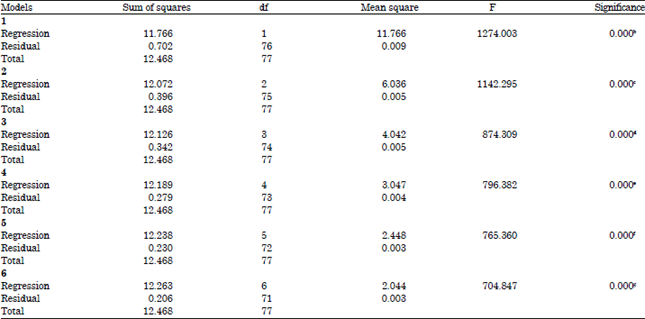
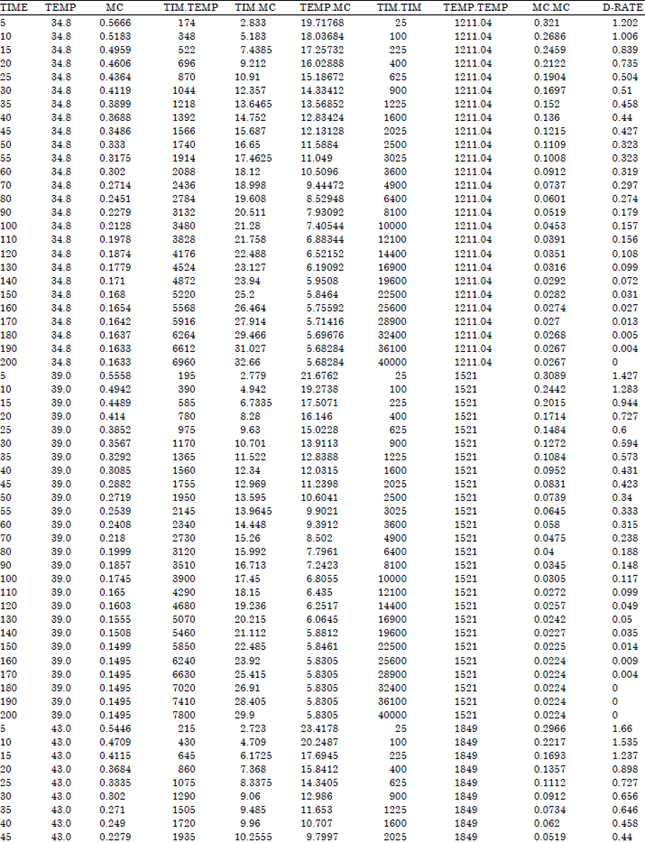
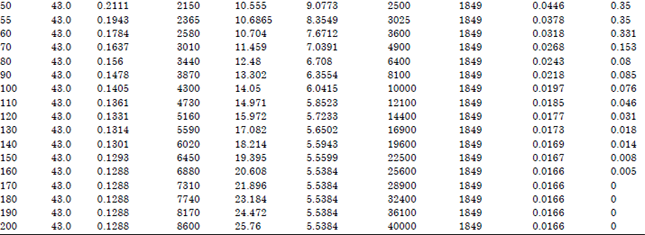
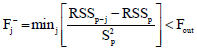Research Article
On the Adequacy of Variable Selection Techniques on Model Building
Department of Mathematics and Statistics, Faculty of Physical Science and Information Technology, University of Port Harcourt, Nigeria
O. P. Efezino
Department of Mathematics and Statistics, Faculty of Physical Science and Information Technology, University of Port Harcourt, Nigeria