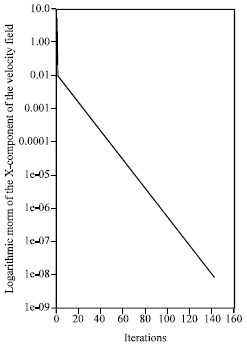
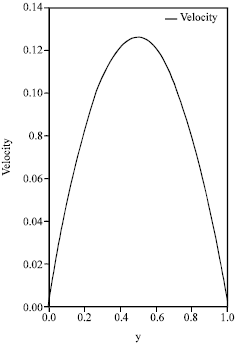
Research Article
Passive Scalar Advection in Micro Fluidic Device
Department of Basic Science, Primeasia University, Bangladesh
G. M. Talukder
Department of Basic Science, Primeasia University, Bangladesh
G. M. Alam
Department of Mathematics, University of Business and Technology (BUBT), Bangladesh
M. K. Alam
Department of Physics, Bangladesh University of Engineering and Technology, Bangladesh
M. J. Alam
Department of Mathematics and Statistics, Memorial University of Newfoundland, Canada