Research Article
Central Limit Theorem for the Sum of a Random Number of Dependent Random Variables
Department of Mathematics, Shanghai Jiao Tong University, Shanghai 200240, China
LiveDNA: 86.3920
The classical central limit theorem is considered as the heart of probability and statistics theory which has a number of applications (Lehmann, 1999; DasGupta, 2008). The assumption of independence for a sequence of observations X1,X2,... is usually a technical convenience. Real data always exhibit some dependence and at least some correlations at small lags (Choi, 2004; Omekara, 2008; Dossou-Gbete et al., 2009; Osareh and Shadgar, 2009; Camminatiello and Lucadamo, 2010). One intensively studied class of dependence is the m-dependence case (Romano and Wolf, 2000; Christofides and Mavrikiou, 2003; Chaubey and Doosti, 2005; Francq and Zakoian, 2005) in which random variables are independent as long as they are m-step apart. More general measures of dependence are referred to as mixing conditions which are derived from the estimation of the difference between distribution functions of averages of dependent and independent random variables. Various mixing conditions have been proposed by Bradley (2005), Balan and Zamfirescu (2006), Kaminski (2007), Ould-Said and Tatachak (2009). The recent text book of DasGupta (2008) contains a survey of some related topics with an eye on statistics.
Recently, the exact value of difference between characteristic functions of sums of dependent and independent random variables is computed to derive central limit theorems for certain class of dependent random variables by Kaminski (2007). This class has some appealing physical interpretations and can be used to describe systems which are globally determined but locally random. His two main results are restated as follows.
Theorem 1: Let{Xi}i≥1 be a sequence of identically distributed random variables such that E|X1|2+ε<+∞ for some ε>0. Let Var(X1) = σ2 and ε1 be a positive number such that ε1<ε/(2(1+ε)). Denote by ![]() the partial sum. Suppose that for sufficiently large k, the inequality:
the partial sum. Suppose that for sufficiently large k, the inequality:
 | (1) |
holds, where v1,...,vj is any choice of indices such that kε1<v1<...<vj≤k. Then:
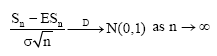 | (2) |
where ![]() denotes convergence in distribution to standard normal distribution.
denotes convergence in distribution to standard normal distribution.
Theorem 2: Let {Xi}i≥1 be a sequence of identically distributed random variables such that E|X1|2+ε<+∞ for some ε>0. Let Var (X1) = σ2 and ε1 be a positive number such that ε1<ε/(2(1+ε)) Suppose that for sufficiently large k:
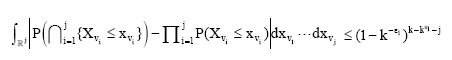 | (3) |
where v1,...,vj is any choice of indices such that kε1<v1<...vj≤k. Then:
| (4) |
The aim of this study is to extend Theorem 1 and 2 in another direction, that is, consider the central limit theorem for partial sum of a random number of {X1}. This question is critical not only in probability theory itself but in sequential analysis, random walk problems, Monte Carlo methods, etc. Central limit problems for the sum of a random number of random variables have been addressed in the study of Korolev (1992), Silvestrov (2006), Przystalski (2009) and Hung and Thanh (2010).
The main results are stated as follows.
Theorem 3: Let {Xi}i≥1 be a sequence of identically distributed random variables such that E|X1|2+ε<+∞ for some ε>0. Let Var (X1) = σ2 and ε1 be a positive number such that ε1<ε/ (2(1+ε)). Denote by![]() the partial sum. Let {Nn}n≥1 denote a sequence of positive integer-valued random variables such that
the partial sum. Let {Nn}n≥1 denote a sequence of positive integer-valued random variables such that
 | (5) |
where, {ωn}n≥1 is an arbitrary positive sequence tending to +∞ and ω is a positive constant. Suppose that for sufficiently large k, the inequality:
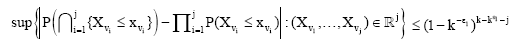 | (6) |
holds, where v1,...,vj is any choice of indices such that kε1<v1<...<vj≤k. If (A1) there exists some k0≥0 and c>0 such that, for any λ>0 and k0:
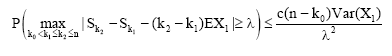 | (7) |
and (A2) Cov (Xi,Xj)≥0 for all i and j, then:
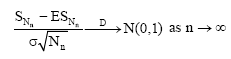 | (8) |
Theorem 4: Let {Xi}i≥1 be a sequence of identically distributed random variables such that E|X1|2+ε<+∞ for some ε>0. Let Var (X1) = σ2 and ε1 be a positive number such that ε1<ε/ (2(1+ε)). Let {Nn}n≥1 denote a sequence of positive integer-valued random variables such that:
| (9) |
where, {ωn}n≥1 is an arbitrary positive sequence tending to +∞ and ω is a positive constant. Suppose that for sufficiently large k, the inequality:
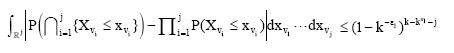 | (10) |
holds, where v1,...,vj is any choice of indices such that kε1<v1<...<vj≤k. If (A1) there exists some k0≥0 and c>0 such that, for any λ>0 and n>k0:
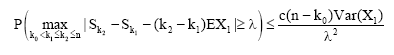 | (11) |
and (A2) Cov (Xi,Xj)≥0 for all i and j, then:
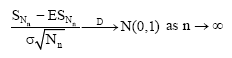 | (12) |
Here are some remarks for Theorem 3 and similar comments may apply to Theorem 4. Firstly, note that the assumption (A1) is for sufficiently large index of sequence Xi, i.e., {Xi}i>k0. Secondly, if {Xi}i≥1 is independent, then (A1) automatically holds for k0 = 0 and c=1 by using the Kolmogorov inequality Billingsley (1995). Therefore, the assumption (A1) may be regarded as a relaxed kolmogorov inequality. Thirdly, the assumption (A2) says that each pair Xi, Xj of {Xn}n≥1 are positively correlated. In view of the independent case studied in previous work, it seems likely that the assertion of Theorem 3 still holds when ω is a positive random variable.
Proof: In the sequel, the proof of Theorem 3 is provided and that of Theorem 4 is left for the interested reader.
Without loss of generality, assume that Xi are centered at 0, i.e., EX1 = 0. Let 0<η<1/2. From Eq. 5 it follows that there exists some n0, for any n≥n0:
| (13) |
For any x![]() :
:
 | (14) |
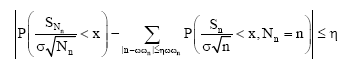 | (15) |
Let n1 = [ω(1-η)ωn] and n2 = [ω(1+η)ωn]. Since ωn tends to infinity, then n1≥k0 for large enough n. Note that![]() . Therefore, for |n-ωωn|≤ηωωn:
. Therefore, for |n-ωωn|≤ηωωn:
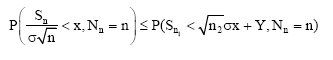 | (16) |
where:
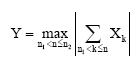 | (17) |
Likewise:
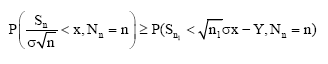 | (18) |
Involving the assumption (A1) and Eq. 17,
| (19) |
the right-hand side of which is less than 1 when η is small enough.
Denote by E the event that ![]() . By virtue of Eq. 15, 16 and 19:
. By virtue of Eq. 15, 16 and 19:
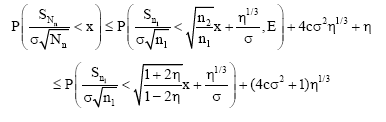 | (20) |
Similarly, from Eq. 15, 18 and 19 it follows that:
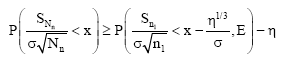 | (21) |
Using (19), (21) and the assumption (A2):
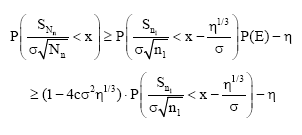 | (22) |
where, the first inequality is due to an application of the FKG inequality (Alon and Spencer, 2008).
Now by Theorem 1:
 | (23) |
where, Φ (x) is the standard normal distribution function. Thus, the proof of Theorem 3 is completed by combining Eq. 20, 22 and 23.
The central limit theorem for dependent random variables is one of the most active areas of research over the past decades. In this study, the central limit theorems for the sum of a random number of certain classes of dependent random variables are treated. The dependency structure may be reflected in some physical phenomena. Other issues such as the convergence rates and other dependent structures are possible future research.