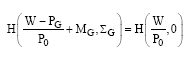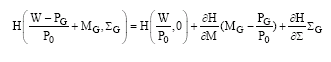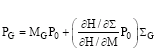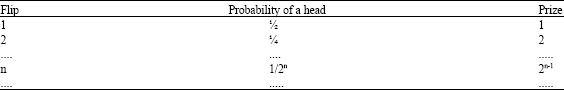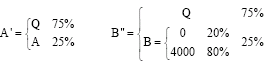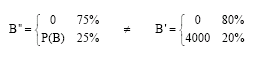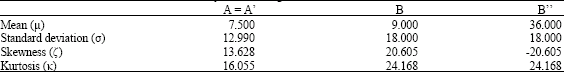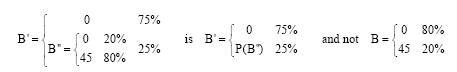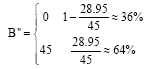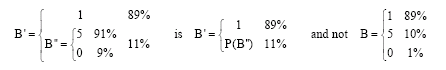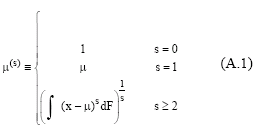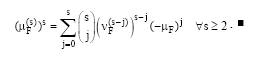Research Article
An Ordinal Utility of Moments for Decisions under Uncertainty
Universita di Bologna, Dip. MatemateS, viale Filopanti, 5, 40126 Bologna, Italy
Carlo D`Adda
Universita di Bologna, Dip. Scienze Economiche, Strada Maggiore, 45, 40125 Bologna, Italy