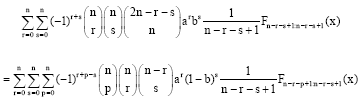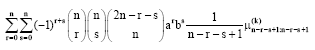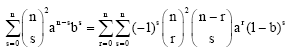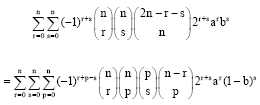Research Article
Some General Identities among Single Moments of Order Statistics
Department of Statistics, Faculty of Mathematical Sciences, University of Delhi, Delhi-110007, India
LiveDNA: 91.31039
S.K. Singh
Department of Statistics, Faculty of Mathematical Sciences, University of Delhi, Delhi-110007, India