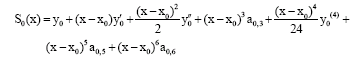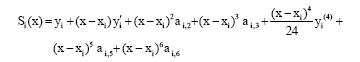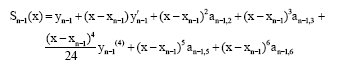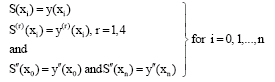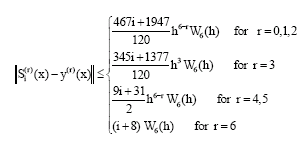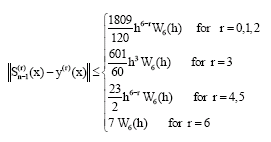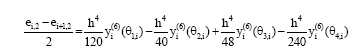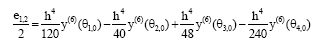Research Article
Lacunary Spline Solutions of Fourth Order Initial Value Problem
Department of Mathematics, College of Science, University of Sulaimani, Sulaimani, Iraq
LiveDNA: 964.3832
R.G. Karem
Department of Mathematics, College of Science, University of Sulaimani, Sulaimani, Iraq