Research Article
Selection of a NLR-Model by Re-Sampling Technique
Department of Mathematics, College of Science, Qassim University,P.O. Box 6644, Buriedah 51452, Kingdom of Saudi Arabia
Mathematical modeling of water flow in unsaturated natural soils leads to partial differential equation-Richard’s equation (Kutilek and Nielsen, 1994). To solve this equation one needs the description of the relationships between soil moisture content, hydraulic conductivity and capillary pressure. The moisture retention characteristic (the relation between water content Θ and pressure head h) can be measured for natural soils. A variety of parametric models have been proposed to describe MRC. All these models are NLR-models, which are able to describe the S-shaped retention curve.
A well known MRC model was studied and moreover a now widely used class of functions for parametrizing measured soil water characteristics
| (1) |
is presented, where α, n and m are positive parameters defining the MRC’s shape (Van Genuchten, 1980; Vereecken et al., 1989). If we consider the saturated water content Θs and the residual water content Θr as parameters too, we will have a MRC model with five parameters, which have to be estimated from observed soil water retention data and this model is denoted by (VG1).
In King (1965), the following model with five real parameters Θs, h0, b, ε and γ is suggested
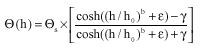 | (2) |
where, b having negative values and this model denoted by (K1).
| Table 1: | Some variants of van Genuchten model (VG1) and King model (K1). |
In El-Shehawy (2008), some special cases of the models (VG1) and (K1) with fewer parameters are studied. Table 1 indicates to these special cases (VG2), (VG3), (VG4) and (VG5) of the model (VG1) and also the model (K2) as a special case of the model (K1).
The model selection in El-Shehawy (2008) is executed by using the simulation study, which based on hundred sets of simulated data and the measures of non-linearity (curvature, bias and skewness).
The results of analyzing experimental data using a parametric model may heavily depend on the chosen model. It is unknown whether a certain regression model describes the unknown true regression function sufficiently well.
In this study, we propose computational tools in S-Plus for the adequate selection of NLR-models based on cross-validation and bootstrap.
The aim of the proposed technique in this study is to select the best parametric NL-model, to compare the results of the used method of the selection with the results of other selection methods, to indicate the caused parameter of this nonlinearity and finally to avoid this defect.
DESCRIPTION OF RE-SAMPLING TECHNIQUE
Let us consider a general NLR-model
| (3) |
where, yij is the values of the response variable Y at fixed values xi of exploratory variables (nonrandom design points). Here, the real valued function f(., β) is expectation function and it is known up to a P-dimensional vector of parameters β = (β1, β2, ..., βp) ε RP and this function is twice continuously differentiable in β. Moreover, the random perturbations εij (the measurement errors) are uncorrelated random variables with zero mean and unknown variance σ2, which do not depend on xi. Given the data
| (4) |
the estimation of the regression function f reduces to estimate its parameters.
If the object of the analysis is primarily the estimation of the regression function, that is, of the values of the regression function itself over a region U of interest, then the weighted cross-validation criterion will be a convenient criterion characterizing the performance of the model f (x, β) (Bunke et al., 1998, 1999):
| (5) |
Here, ![]() denotes the least squares estimator (LSE), which is calculated from the (n-1) observations left after deleting the observation (xi, yij), with xi ∈
denotes the least squares estimator (LSE), which is calculated from the (n-1) observations left after deleting the observation (xi, yij), with xi ∈ ![]() . Thereby we assume that the (ordered) values xr≤...≤xs of the independent variable are in the region.
. Thereby we assume that the (ordered) values xr≤...≤xs of the independent variable are in the region.
If ![]() = [a, b] is the interval of the interest with a≤xr≤...≤xs≤b, then one will use weights
= [a, b] is the interval of the interest with a≤xr≤...≤xs≤b, then one will use weights
| (6) |
with and ![]()
If one would not like to specify the interval ![]() = [a, b], then a = x1 and b = x2 should be the standard values. The use of a criterion like (5) is justified by the fact, that it estimates the weighted sum of the actual squared prediction errors. The cross-validation criteria (5) will be adequate, if prediction or estimation of the regression function (here the MRC) is a primary objective of the data analysis.
= [a, b], then a = x1 and b = x2 should be the standard values. The use of a criterion like (5) is justified by the fact, that it estimates the weighted sum of the actual squared prediction errors. The cross-validation criteria (5) will be adequate, if prediction or estimation of the regression function (here the MRC) is a primary objective of the data analysis.
Following Bunke et al. (1998, 1999), the model selection could be done by using the cross-validation criteria (5) in three steps:
| • | List alternative models |
| • | Select among these models |
| • | The data analysis is then done with the estimated regression function |
As an alternative to the Ordinary Least Squares Estimator (OLSE) in view of possibly heteroscedastic variances ![]() a (non-homogeneous) variance model could be chosen and a corresponding Weighted Least Squares Estimator (WLSE) should be used. Furthermore, it is possible to asses with a procedure in S-Plus the accuracy of the parameter estimations using re-sampling methods.
a (non-homogeneous) variance model could be chosen and a corresponding Weighted Least Squares Estimator (WLSE) should be used. Furthermore, it is possible to asses with a procedure in S-Plus the accuracy of the parameter estimations using re-sampling methods.
With respect to the goodness of fit, one can use the criteria ![]() , where
, where
| (7) |
ACCURACY AND PROFILE
Estimates (for instance parameter estimates) will be only of value, if they are complemented by an assessment of their accuracy. Therefore, statistical packages offer the possibility to calculate characteristics like the standard deviation or confidence intervals. These calculations are often based on linear models (linearization) or asymptotic theories (Bates and Watts, 1988; Seber and Wild, 2005). In case of NLR-models combined with typical small data sets these calculated results may differ significant from the true values. Especially strong nonlinear parameters may have confidence intervals which will be essentially differing from the calculated intervals using a linearization of the NL-model. To overcome these difficulties it is possible to use re-sampling methods -bootstrap- or corrected versions of the confidence intervals based on nonlinear theories.
Accuracy of Parameter Estimates
The bootstrap is a re-sampling method that tries to mimic the (in general unknown) distribution of the observations (measurement error) by generating artificial independent bootstrap samples from the fitted model. The estimates of the model parameters are repeatedly calculated for these bootstrap samples. The accuracy of the original estimates in inferred from the empirical distribution of the bootstrap estimates. In Bunke et al. (1998, 1999), a moment oriented bootstrap procedure, which is based on a non-linear transformation (Box-Cox-transformation) to get nearly normally distributed residuals and on the estimation of variance (second moment) of this distribution, is used. The bootstrap can be applied when a regression and variance model were selected. Then it is possible to generate bootstrap samples based on realizations of corresponding normally distributed pseudo random numbers and to compute confidence intervals and some other measures of accuracy (variance, bias and mean absolute relative error) based on this simulation.
Profiles of Parameter Estimates
Another way to get exact confidence intervals for a single component of the parameter vector is the use of so called profile t functions and plots (Bates and Watts, 1988; Seber and Wild, 2005). Plots of the profile t function τ(βr) provide exact likelihood confidence intervals of the parameters and in addition, reveal how nonlinear the estimation situation for the corresponding parameter is.
The profile t function represents the profile of the residual sum of square function as a function of a single component of the parameter vector in a neighborhood of the estimated parameter vector.
In case of a linear regression model (LR-model) the squares root of this residual sum of square function-the profile t function- is a linear function δ(βr) of the corresponding component βr of the parameter vector β. Moreover, the plot of this function against the component would be a straight line.
For a nonlinear component of the parameter vector in a NLR-model the plot of the profile t function will be curved and the amount of curvature gives some information about the nonlinearity of the model and of the component of the parameter vector. Using these profiles it is possible to construct exact confidence intervals for the components of the parameter vector of the model under consideration.
In this section we present the results of the model selection with re-sampling technique and assessment of accuracy of parameter estimates.
Model Selection with Re-Sampling
Now, we consider the model selection based on the weighted cross-validation criterion (5). Using this criterion we will look for a retention model, which minimizes the weighted sum of the actual squared prediction errors. That means, we look for a model, which is stably able to predict values of the retention function based on the given data situation.
We consider the first simulated data set SIMUL_1 of sand (El-Shehawy, 2008), which is given in Table 2.
Since the simulation uses a homogenous error variance, we consider only all combinations of retention models with a homogenous variance for the measurement errors.
Table 3 contains the ranking of the studied models with respect to the RSS criterion and the CV criterion. These results are obtained by using the S-PLUS procedure in Appendix A.
We remark that the model (VG5) is not flexible enough and therefore convergence problems during the calculation of the CV value occur.
An application of the cross-validation approach to our problem would lead to the selection of the model (VG4) with four parameters.
| Table 2: | The first simulated MRC-data for sand |
 | |
| Table 3: | Ranking of retention models with respect to CV and RSS for the first simulated data |
 | |
Referring to El-Shehawy (2008), if we are is interested in the model (VG4) with four parameters, we will try to improve the problematic qualities by the suggested re-perarameterization (RVG4) of the model (VG4) through replacing the parameter n by .
Since the values of RSS and CV are independent of parameterization, then the model (RVG4) is identical with respect to these criteria with the model (VG4). The models (VG1) and (K1) with five parameters are very flexible and are having optimal values with respect to RSS.
These results are neither depending on the used simulated data set of a soil nor on the simulated type of soil. As a rule, we get optimal values with respect to the cross-validation criterion for the model (VG4) and its re-parametrization (RVG4). Moreover, the models (VG1) and (K1) are having the best fit with respect to the values of RSS.
If we consider data sets with a possibly inhomogeneous variance structure, we will obtain similar ranking of retention models in combinations with an inhomogeneous variance model. Referring to Bunke et al. (1999), variance modeling can improve the parameter estimation for a given model using the weighted least squares in place of the ordinary least squares.
Assessment of Accuracy of Parameter Estimates
The assessment of accuracy is a necessary part of the parameter estimation for a given NLR-model. We will consider accuracy statistics for some parameters of the model (VG4) and its re-parametrization (RVG4).
Table 4 gives such statistics for the parameters α, n and ![]() of the model (VG4) and (RVG4), respectively combined with the simulated data SIMUL_1 of sand.
of the model (VG4) and (RVG4), respectively combined with the simulated data SIMUL_1 of sand.
| Table 4: | Accuracy statistics for α, n and |
 | |
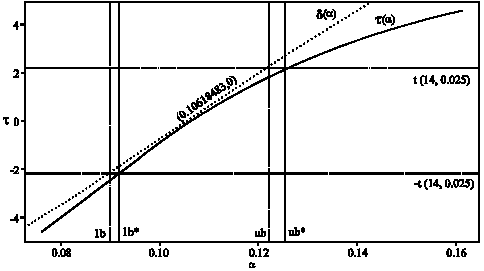 | |
| Fig. 1: | Profile t function τ(α) and linear profile δ (α) for the parameter α in the model (VG4) with respect to the first simulated set of sand |
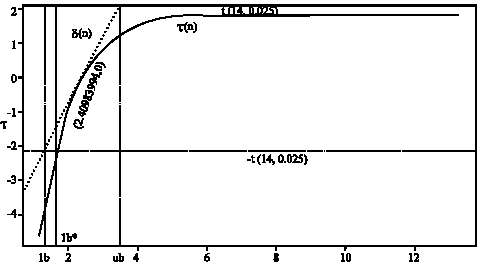 | |
| Fig. 2: | Profile t function τ (n) and linear profile δ (n)for the parameter n in the model (VG4) with respect to the first simulated set of sand |
These statistics are obtained by using the S-PLUS procedure in Appendix B. This table contains the estimated values of the corresponding parameter of the model and the used data set and several 95% confidence intervals CI, CIb and CI*.
We start with classical asymptotic results, which are based on a linearization of a NL-model. The confidence interval CI with lower bound lb and upper bound ub shows these results. The calculations of these confidence intervals are based on the theory of LR-models.
In case of a parameter, which has near linear behavior, this linear approximation of a NLR-model provides adequate inferential results.
Unfortunately, in a nonlinear analysis and parameters with strong nonlinear behavior combined with typical small data sets this approximation will be woefully inadequate. For example, the parameter α shows weak nonlinear behavior, the parameter n has stronger properties of nonlinearity with respect to its estimation. Referring to El-Shehawy (2008), the corresponding parameter ![]() of the re-parameterization (RVG4) has improved properties.
of the re-parameterization (RVG4) has improved properties.
In the second attempt to improve the accuracy statistics based on a bootstrap simulation we calculated a 95% confidence interval CIb of the estimated parameter. The calculation of this confidence interval is based on bootstrap sample of hundred data sets generated with NLRCHOICE (Bunke et al., 1998, 1999). These accuracy statistics are inferred from the empirical distribution of the estimated parameters for this bootstrap sample.
The third possibility is the calculation of an exact likelihood interval CI* with lower bound lb* and upper bound ub*. That means, if we are interested in this exact interval for the nonlinear parameter βr, we will use the profile t function τ(βr) to correct the asymptotic confidence interval CI.
In Fig. 1 and 2, which are obtained by using the S-PLUS procedure in Appendix B, the curves (solid) show the profiles τ(α) and α(n), the dotted lines are the linear approximations δ(α) and δ(n) and the lines (dashed) describe the construction of 95% exact confidence intervals for the parameters α and n, respectively.
In case of the near linear parameter we get only a slight modification CI* of the classical asymptotic confidence interval CI, but in case of the parameter n with strong nonlinear estimation behavior the exact confidence interval CI* is completely different from CI. This exact confidence interval CI* is unbounded above. That means, for typical data sets frequently very large values of n will be estimated.
Model selection of NLR-models depends on the main aim of the analysis. A retention model has to be able to describe the typical S-shaped retention curve.
If one is interested in the best fitting model, very flexible models with more parameters should be used. As a criterion ordinary or in case of heteroscedasticity weighted least squares can be used. In case of a retention curve the models (VG1) and (K1) with five parameters are optimal with respect to the goodness of fit.
If one is primary interested in the prediction of future values of the depending variable -here water content-a cross-validation criterion like will be used. This criterion describes the stiffness of the model that means the ability to predict values of the depending variable based on the given data. Optimal with respect to the cross-validation criterion is the model (VG4) with m = 1.
The results of model selection are identical with the corresponding results which were obtained by the simulation studies or the calculation of measures of nonlinearity.
Using profile t functions, we note that:
| • | The selected model (VG4) has a strong nonlinear parameter n and also it has a possible appropriate re-parameterization (RVG4) with respect to this parameter. |
| • | It is possible to correct classical confidence intervals of estimated parameters, which having clear nonlinear behavior. |
APPENDIXES
A. S-PLUS Procedure for Model Selection
 |
B. S-PLUS Procedure for Calculating the Exact Confidence Intervals and the Profile of the Parameters
 |