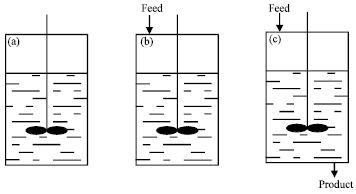
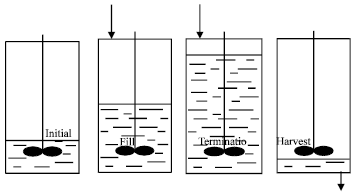
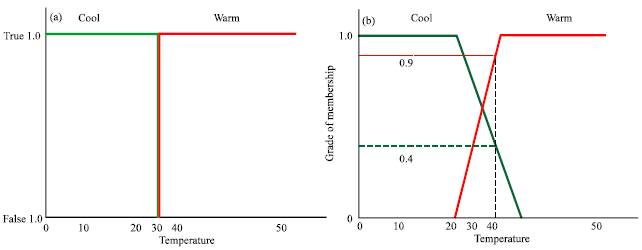
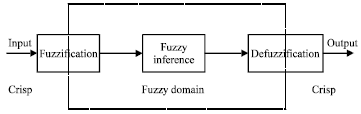
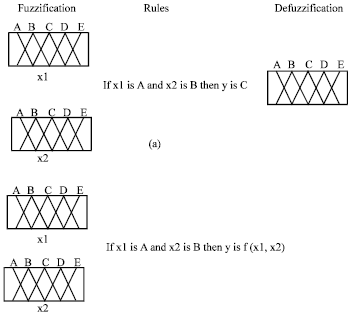
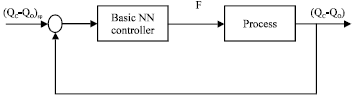
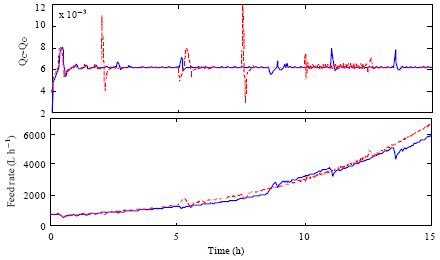
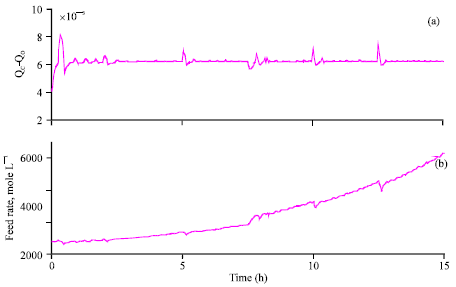
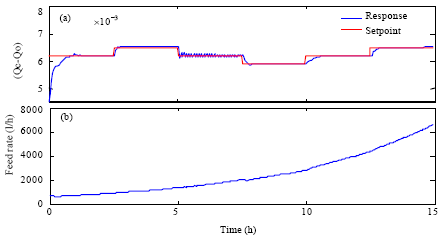
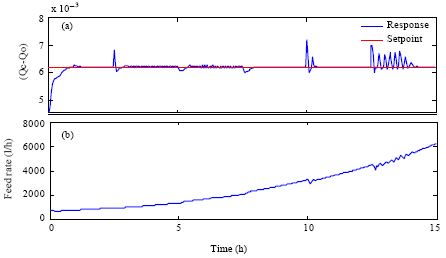
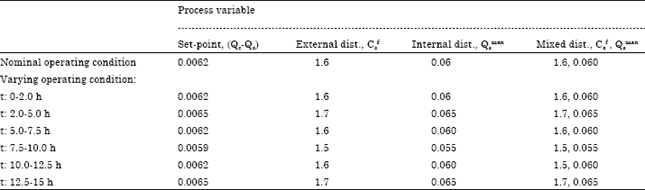
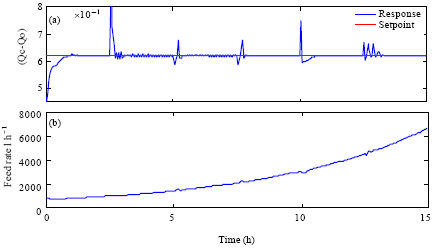
Research Article
Advanced Control Technique for Substrate Feed Rate Regulation of a Fed Batch Fermentation
Department of Mechatronics Engineering, Faculty of Engineering, International Islamic University, Malaysia
Hizbullah
Universitas Syiah Kuala Banda Aceh, Indonesia
Noor Mohammad
Department of Biotechnology Engineering, Faculty of Engineering, International Islamic University, Malaysia
M. Jakir H Khan
Department of Biotechnology Engineering, Faculty of Engineering, International Islamic University, Malaysia